Optical detectors, noise, and the limit of detection
Measuring light
- Detection of light can be decomposed in three simplified steps:
- conversion of light to free electrical charge-carriers
- conversion of current to voltage
- measurement of voltage.
- Light sensors for converting photons to voltages fall into two main categories:
- array detectors that use the photovoltaic effect (e.g. charge-coupled device CCD, or complementary metal-oxide semiconductor CMOS, cameras)
- point detectors that rely on the photoelectric effect (e.g. photodiodes or photomultipliers tubes PMT).
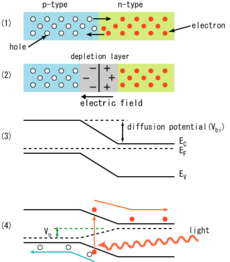
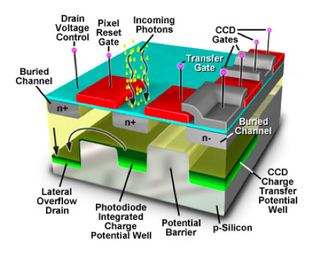
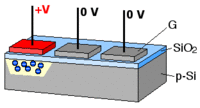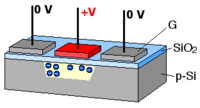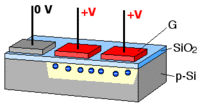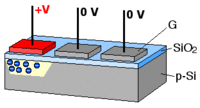
CCDs and the photovoltaic effect
What is commonly dubbed a "CCD camera" in digital imaging language is the combination of
- a photoactive region where an array of light-sensing pixels (p-doped MOS or active CMOS capacitors) convert incoming photons into electron charges at the semiconductor-oxide interface of the detection layer;
- a transmission region where charge-coupled devices per se move electric charges laterally along shift registers by transferring them sequentially between capacitive bins; gate voltages dictate the travel of charge packets;
- a charge-to-voltage converter: the last capacitor in the array dumps its charge into an amplifier that converts the charge into a voltage. The sequence of voltages is in turn sampled, digitized, and stored in memory by the CCD camera.
Frame transfer methods allow exposure and readout in parallel.
|

|
|
|
In a CCD camera,
- the imager is essentially an array of photodiodes,
- each pixel stores charges in proportion to the number of photons absorbed,
- the photon-to-charge conversion efficiency depends on the wavelength,
- each well has finite storage capacity (hence pixel saturation),
- the size and density of pixels determines the resolution and field of view in the image plane,
- pixels are as small as ~3 µm.
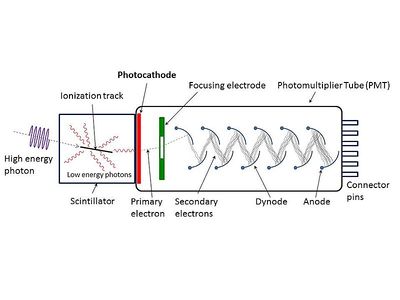
PMTs and the photoelectric effect
Noise sources in optical detectors
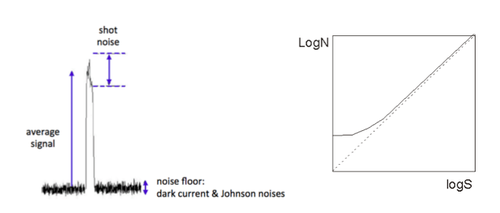
The maximum information you can extract from an image is limited by its signal-to-noise ratio (SNR). With signal defined as the amount of light incident upon the detector per unit time, noise can be seen as the “disturbance” on the signal level that hinders an accurate measurement.
Examining the sources of noise in your optical detector, both fundamental and technical, and understanding which contributions have the greatest impact on the uncertainty of your measurement, will be central to optimizing the quality of your results and conclusions.
- Optical detectors are subjected to
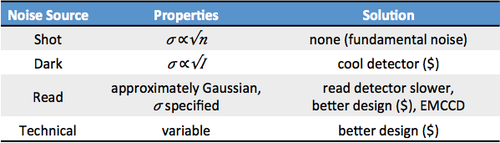
- Optical shot noise (Ns): inherent noise in counting a finite number of photons per unit time
- Dark current noise (Nd): thermally induced “firing” of the detector
- Read noise, or Johnson noise (NJ): thermally induced current fluctuation in the load resistor, while counting photons
- Background light from blackbody radiation
- 1/f noise, or flicker noise
- Technical noise due to various imperfections, usually corrected by better (and more expensive!) design.
Let's look into some of these sources of noise:
Poisson shot noise
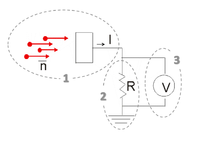
As photons are emitted independently of each other, the events of photon arrival at the detector are statistically independent, or “uncorrelated”. Although the mean number of photons $ \bar n $ arriving per unit time is constant on average, at each measurement time interval t, the number of detected photons does vary.
- The statistical fluctuation of uncorrelated random events obey Poisson statistics.
- The probability of observing $ n $ photons is:
- $ P (n| \bar n)= e^{-{\bar n}} {{\bar n}^n \over {n!}} $
- A key property of data following a Poisson distribution is that their standard deviation is equal to the square-root of their mean:
- $ \sigma_n = \sqrt {\bar n} $
- Thus the signal-to-noise ration associated with a Poisson distribution also increases with square-root of the intensity!
- $ SNR_{Poisson} = {\bar n \over {\sigma_n}} = \sqrt {\bar n} $
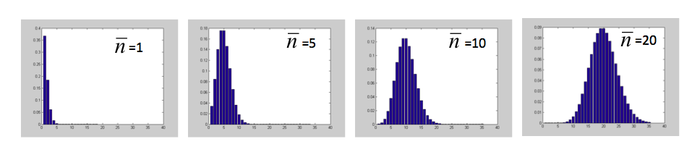
| Poisson statistics of uncorrelated events | |||
| Distribution of uncorrelated events of mean $ \bar n $ varying from 1 to 20: | |||
| mean: $ \bar n = {1 \over M} \sum_1^M {n_i} $ | variance: $ \sigma_n^2 = {1 \over M} \sum_1^M {{(n_i - \bar n)}^2} $ | standard deviation: $ \sigma_n = \sqrt {\bar n} $ | |
- The shot noise in photon count (on $ \bar n $) results in shot noise in electrical current (on I ):
- $ \left \langle I_{signal} \right \rangle = \eta q \bar n / \Delta t $
- where $ \bar n $ is the number of photons incident, $ \Delta t $ is the acquisition time, q is the charge of an electron (q = 1.6 x 10$ ^{-19} $ C), and η is the quantum efficiency of the detector.
- hence $ \left \langle I_{noise} \right \rangle = \eta q \sqrt {\bar n} / \Delta t $
- or $ \left \langle I_{noise}^2 \right \rangle = {\left ( \eta q / \Delta t \right )}^2 \bar n $
- and $ \left \langle I_{noise}^2 \right \rangle = \left ( \eta q / \Delta t \right ) \left \langle I_{signal} \right \rangle $
- Now introducing four important definitions:
- Signal power: $ S = \left \langle I_{signal}^2 \right \rangle R $,
- Noise power: $ N = \left \langle I_{noise}^2 \right \rangle R $,
- Signal-to-noise ration SNR: $ S = Signal Power / Noise Power = S / N $,
- Noise equivalent power NEP: signal power at which SNR = 1,
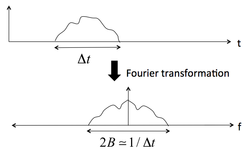
- we obtain an expression for the shot noise Ns in Fourier space $ N_s = \left \langle I_{noise}^2 \right \rangle R = 2 R \eta q B \left \langle I_{signal} \right \rangle $
- with 2B the bandwidth (in hertz) over which the noise is considered, i.e. the effective bandwidth of an integrating filter of sampling time Δt.
Relating current $ I $ to optical power P
- Calling P the optical power
- $ P = \bar n \left ( {{hc \over \lambda}}\right )/ \Delta t $
- and remembering $ \left \langle I \right \rangle = \eta q \bar n / \Delta t $
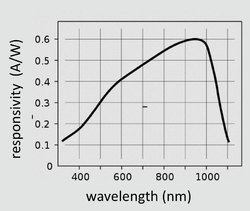
- one derives the detector's responsivity indicated in spec sheets
- $ {I \over P} = {\eta q \lambda \over hc} $
- Besides, with $ {\left ( {S \over N} \right )}_{current} = {\left \langle I_{signal} \right \rangle \over \sqrt {\left \langle I_{noise}^2 \right \rangle }} $ and $ \left \langle I_{noise}^2 \right \rangle R = 2 \eta q B \left \langle I_{signal} \right \rangle $,
- we obtain $ {\left ( {S \over N} \right )}_{current} = {\sqrt {\left \langle I_{signal} \right \rangle \over 2 \eta q B}} = {\sqrt {P \lambda \over 2 h c B}} $
- and $ {\left ( {S \over N} \right )}_{power} = {P \lambda \over 2 h c B} = \bar n $
Dark current noise
- The ideal photoelectric or photovoltaic device does not produce current (electrons) in the absence of light. However, thermal effect results in some probability of spontaneous production of free electrons (in the absence of photons). This effect is measured by the dark current amplitude of the device: $ \left \langle I_d \right \rangle $.
- The magnitude of dark current decreases with decreasing temperature. Dark current noise can thus be minimized by cooling the detector.
- The average dark current is constant at constant temperature, and it can be subtracted from the signal, but the electron generated fluctuate in time according to Poisson statistics, similar to the fluctuation of the signal photons. From our discussion of photon shot noise, we have readily:
- $ N_d = 2 R \eta q B \left \langle I_d \right \rangle $
Read noise
- Read noise or Johnson noise originates from the temperature dependent fluctuation in the load resistance R of the transimpedance detection circuit. The term "read noise" tends to be a catch-all for any noise that arises during the process of counting the electrons.
- In a CCD camera, note that defects in the semiconductor cause read noise to vary across pixels.
- Consider a simple dimensional analysis:
- thermal energy: $ k_B T/2 $
- thermal power: $ N_J = {k_B T/ {2 \Delta t}} = k_B TB $
- and since the power of Johnson the noise current is expressed also as $ \left \langle I_J^2 \right \rangle R $
- $ I_J = \sqrt {{k_B TB \over R}} $
- Like shot noise, Johnson noise is fundamental and unavoidable. Running the detector slower, or cooling it, reduces read noise effects.
The case of CCD cameras
- In addition to shot noise (Ns limits the SNR set by Poisson photon counting statistics), dark current noise (Nd), and Johnson noise (NJ which can be reduced by cooling systems surrounding the CCD), a CCD is subjected to readout noise Nr: the noise that amplifier circuits introduce during the transfer and digitization of the CCD charges.
- The electron-multiplying charge-coupled device (EMCCD) technology amplifies electrons before the amplifier circuitry by impact ionization on the chip (in a similar way to an avalanche photodiode). This approach overcomes readout noise, but introduces “salt and pepper” noise; even though EMCCD detector have a resolution to a single molecule emission, their images look grainy.
Quantization
- Images from CCD cameras are also subject to quantization noise, stemming both from pixel and from bit-depth quantization dictates.
| Quantization in CCD cameras | |||
| Each pixel gets assigned a single integer-value intensity, which is the average of the light signal reaching its surface area.
It is thus judicious to try and match the pixel size to the optical system resolution. As a rule of thumb, an adequate pixel size is given by the formula
|
The number of intensity levels encodable in each pixel depends on the bit-depth of the CCD camera.
A 12-bit grayscale CCD describes the signal by ascribing a number in the [0 - (212-1)] range to each pixel. | ||
Binning
The CCD pixel size influences its resolution:
- Too large pixels may not capture spatial granularity of specimen and not resolve the image.
- Small pixels increase spatial resolution of the detector, but sometimes to the detriment of SNR: if there is too little light collected per pixel, then the CCD readout circuit noise dominates the signal.
- Pixel binning can be applied (either at the camera level or during data processing steps) to increase signal and signal-to-noise ratio (even though the electrical readout noise is also multiplied!).
- Decreasing the frame rate of CCD acquisition also reduces the shot noise, relatively, and thus boosts the SNR of images.
Compounding sources of noise
- Uncorrelated sources of noise N such that
- $ \lim_{T \to {+ \infty}} {{1 \over T} \int_{-T/2}^{T/2} (n(t+\tau) - \bar{n})(n(t) - \bar{n})^*\, d\tau} = \left \langle \Delta {n(t+\tau)} \Delta {n^* (t)} \right \rangle = 0 $
- (with $ \tau \ne 0 $ and * denoting the complex conjugate)
- will add in quadrature:
- $ N^2 \propto N_s^2 + N_d^2 + N_J^2 $
Bottom line on optical detector noise
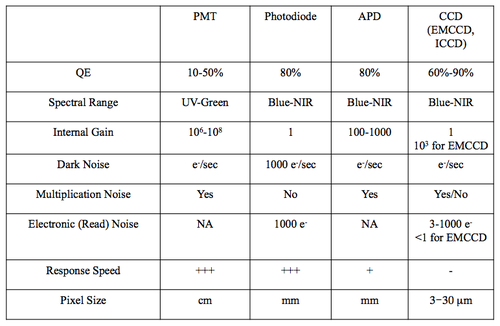
Comparing characteristics of optical detectors
- Key properties of optical detectors are embodied by these specifications:
- quantum efficiency: probability of generating of a photoelectron from an incident photon
- internal amplification: amplification ratio for converting a photoelectron into an output current
- dynamic range: region between the largest and the lowest signal that can be measured linearly
- response speed: time difference and spread between an incoming photon and the output current burst
- geometric form factor: size and shape of the active area and of the detector
- noise.
The chart below compares performance characteristics of four types of light detectors: photo-multiplier tubes (PMT), photodiodes, avalanche photo-diodes (APD), and charge-coupled devices or CCD cameras, including the electron-multiplying (EMCCD) and intensified (ICCD) flavors.
Optical microscopy lab
Code examples and simulations
- Converting Gaussian fit to Rayleigh resolution
- MATLAB: Estimating resolution from a PSF slide image
- Matlab: Scalebars
- Calculating MSD and Diffusion Coefficients
Background reading
- Geometrical optics and ray tracing
- Physical optics and resolution
- Optical aberrations
- Aperture and field stops
- Optical detectors, noise, and the limit of detection
- Manta G032 camera measurements
- Understanding log plots