20.109(F21):M2D6
Contents
Introduction
Today you will begin to assess the data collected from the IPC experiment by assessing the KD and the association / dissociation rates. As a review of the key concepts, consider the simple case of a receptor-ligand pair that are exclusive to each other, and in which the receptor is monovalent. The ligand (L) and receptor (R) form a complex (C), which can be written
$ R + L \rightleftharpoons\ ^{k_f}_{k_r} C $
At equilibrium, the rates of the forward reaction (rate constant = $ k_f $) and reverse reaction (rate constant = $ k_r $) must be equivalent. Solving this equivalence yields an equilibrium dissociation constant $ K_D $, which may be defined either as $ k_r/k_f $, or as $ [R][L]/[C] $, where brackets indicate the molar concentration of a species. Meanwhile, the fraction of receptors that are bound to ligand at equilibrium, often called y or θ, is $ C/R_{TOT} $, where $ R_{TOT} $ indicates total (both bound and unbound) receptors. Note that the position of the equilibrium (i.e., y) depends on the starting concentrations of the reactants; however, $ K_D $ is always the same value. The total number of receptors $ R_{TOT} $= [C] (ligand-bound receptors) + [R] (unbound receptors). Thus,
$ \qquad y = {[C] \over R_{TOT}} \qquad = \qquad {[C] \over [C] + [R]} \qquad = \qquad {[L] \over [L] + [K_D]} \qquad $
where the right-hand equation was derived by algebraic substitution. If the ligand concentration is in excess of the concentration of the receptor, [L] may be approximated as a constant, L, for any given equilibrium. Let’s explore the implications of this result:
- What happens when L << $ K_D $?
- →Then y ~ $ L/K_D $, and the binding fraction increases in a first-order fashion, directly proportional to L.
- What happens when L >> $ K_D $?
- →In this case y ~1, so the binding fraction becomes approximately constant, and the receptors are saturated.
- What happens when L = $ K_D $?
- →Then y = 0.5, and the fraction of receptors that are bound to ligand is 50%. When y = 0.5, the concentration of free calcium (our [L]) is equal to $ K_D $.
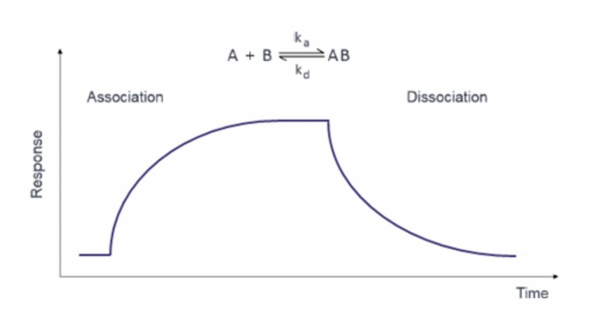
In the BLI experiment, the association rate constant ($ k_a $ or $ k_{on} $) and dissociation rate constant ($ k_d $ or $ k_{off} $) are measured for each concentration of ligand. The $ K_D $ is calculated from these values using the following equation:
$ K_D = k_d/k_a $
In the graph below this relationship is measured as response over time where A = the protein immobilized to the probe and B = small molecule in solution.
Protocols
Part 1: Complete data analysis for BLI assay
Review the short tutorial videos on processing BLI data sets (available here) and kinetic analysis (available here).
- Open your file in the Data Analysis software.
- Save the raw file by clicking the ‘raw file’ button at the bottom.
- Align the baseline along the Y axis by clicking ‘Y-axis alignment’.
- Select the row and indicate it as ‘reference sample.’
- We need to subtract the compound only curve from the (protein + compound) curves at during the experimental analysis. Select the rows (A1-B1) for subtraction and click the ‘subtraction’ button.
- Save the processed file by clicking the ‘process’ button.
- To obtain the kinetic binding values, we will do curve fitting to the preset binding equations. For example, there are set parameters as 1:1 vs 2:1 binding. 1:1 and 2:1 fit means 1 protein to 1 compound binding and 1 protein to 2 compound binding, respectively.
- You will perform the 1:1 fitting operation and save the file.
- You will later analyse these data to see which fitting model is suitable for our kinetic experiment.
Part 2: Review journal article
Read and discuss the following journal article with your laboratory partner:
Amberg-Johnson et al. "Small molecule inhibition of apicomplexan FtsH1 disrupts plastid biogenesis in human pathogens." eLife. (2017) 6:e29865.
The initial experiment presented by Amberg-Johnson et. al. shows the effect of actinonin on apicoplast biogenesis. The apicoplast is an essential plastid organ that is a key target for drug development in research focused on malaria treatment. Actinonin was identified in large-scale screen of compounds known to inhibit growth of parasite. The subsequent experiments completed in this research served to uncover the mechanism-of-action of actinonin is it pertains to disruption of the apicoplast.
In the context of your research, this article focuses on the next step experiments that can be performed after a drug candidate is discovered from a screen. Though you can use this article as guidance as you consider the experiments that could follow your screen, remember that the specific next step experiments should be related to the protein target and drug candidate(s) identified in your project. For this exercise, the focus in on how the data are organized and presented.
In your laboratory notebook, complete the following with your partner:
- Why is the apicoplast a promising target for anti-malarial drug development?
- Why have attempts at developing broadly effective drugs that target the apicoplast been unsuccessful?
- Why is the approach used by the researchers in this article more promising?
- List the figures that are included in the article. For each figure:
- What is the main conclusion / finding in each figure?
- Which panel best supports the main conclusion / finding? Is more than one panel needed to fully support the main conclusion?
- Are you convinced by the data? Do you agree with the main conclusion?
- Are the figures organized in a coherent story?
- Write transition statement that connect each figure to the next. A transition statement should very briefly summarize the findings of a figure and state what those findings motivated the research to do next (ie what is the next experiment?).
Next day: Plot and interpret data from secondary assay