Geometrical optics and ray tracing

Light is an extraordinarily complicated, three dimensional, time dependent phenomenon. Completely describing a light field requires a function that quantifies the intensity, phase, wavelength, and propagation direction of light at every point in space. Needless to say, it can be difficult to conceptualize a light field. Fortunately, there is a simplified model of light that applies in situations where objects that interact with the light field are much larger than the wavelength of the light. The simplified model, called ray optics, offers a good way to understand the function of many systems of lenses, mirrors, filters, and illumination sources. Ray optics can elucidate the function of a complicated optical system with just a few lines, triangles, and simple rules.

The simplicity of ray optics comes at a cost. Ray optics glosses over important details, like diffraction and interference. Thus, ray optics alone does not provide insight into detailed performance characteristics like resolution.

This page introduces ray optics and discusses distortions called optical aberrations that occur as some of the simplifying assumptions go awry. Diffraction and resolution are discussed on a separate page.

Reflection and refraction

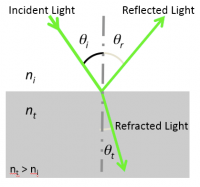
When incident light reaches an interface between two optical media, it can be

• reflected, partly or totally,
• scattered in random directions,
• refracted and thus entering the second medium, and/or
• absorbed partly.

We will limit our seminal discussion of basic geometrical optics to cases where interfaces are non-absorbant and smooth (as opposed to uneven) surfaces giving rise to specular (as opposed to diffuse) reflection and refraction.

Reflection at a boundary

• The law of reflection states that the angle θ_r the reflected ray makes with the normal to the surface is equal to the angle θ_i the incident ray makes with this normal. Incident and reflected rays are in the same plane.

$ \theta_i = \theta_r $

• The law of reflection applies to plane and curved (e.g. spherical) interfaces.

Refraction at a plane boundary

Index of refraction

• The index of refraction $ n $ of a transparent optical medium is defined as the ratio of the speed of light in vacuum, $ c $, by the speed of light in the medium, $ v $.

$ n = c / v $

Snell's law of refraction

• Light incident at an interface between two media of distinct indices of refraction will be partly reflected back into the first medium and partly transmitted to the second medium, or refracted according to the Snell-Descartes law:

$ n_i\ \sin \theta_i = n_t\ \sin \theta_t $

with θ the angle measured from the normal of the boundary, $ n $ the refractive index (which is unitless) of the medium, and the subscripts $ i $ and $ t $ referring to the incident and transmitted light, respectively.

• Snell's law implies that light passing from a medium of lower index to a higher index of refraction ($ n_t > n_i $) bends toward the surface normal ($ \theta_t < \theta_i $), whereas light traveling from a higher index to a lower index of refraction bends away from the normal.

Critical angle and total internal reflection

• From Snell's law of refraction ensues the existence of a critical angle $ \theta_c $ for the incident light ray at which it gets bent by 90^o at the boundary and thus continues traveling along the interface between the two media. Beyond $ \theta_c $ total internal reflection takes place.
• Recalling that $ \sin (90^o) = 1 $, one can derive

$ \theta_c = \sin ^{-1} \left ( {n_t \over n_i} \right ) $

• The phenomenon of total internal reflection is the principle of light transmission via optical fibers, whose core medium is cladded by a distinct medium of lower index of refraction.

Refraction at a spherical boundary

Gaussian optics assumptions

The lens formulas and ray tracing techniques we'll be using will rely on the first-order or Gaussian optics approximations:

• Paraxial (or small-angle) approximation:

$ \theta \approx \sin\ \theta \approx \tan\ \theta $

$ \cos\ \theta \approx 1 $

(These relations obtained from the first-order terms of the polynomial expansions of $ \sin \theta = \theta - {\theta^3 \over {3!}} + {\theta^5 \over {5!}} - ... $ and $ \cos \theta = 1 - {\theta^2 \over {2!}} + {\theta^4 \over {4!}} - ... $ are accurate to 1% if $ \theta < 10^o $.)

• Thin-lens approximation:

$ R << S_o,\ S_i $

with $ R $ defined as the radius of curvature of the lens, $ S_o $ as the distance between the lens and the object, and $ S_i $ the distance between the lens and the image.

• The paraxial and thin-lens assumptions are engineering approximations that allow you to quickly and intuitively understand most optical systems using a simple set of ray tracing rules.
• Deviations from these assumptions result in optical aberrations.
• More on thick lenses can be found in the book 'Optics' by Eugene Hecht (Addison-Wesley​, 2002, ISBN 0805385665).

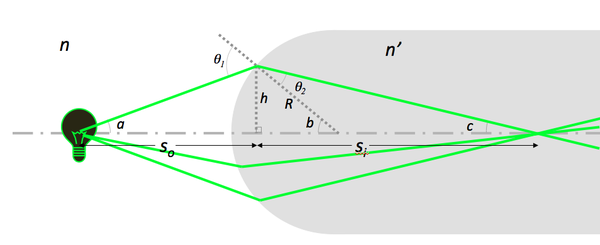
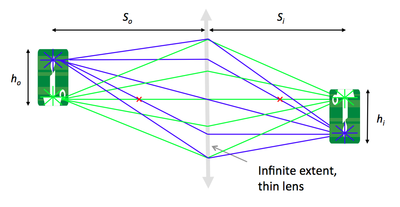
Object and image positions

• Under Gaussian optics conditions, Snell's law predicts the image position of an object formed by a lens:

$ n\ \sin \theta_1 = n'\ \sin \theta_2 $

$ \sin \theta_1 \approx \sin a + \sin b \approx {h \over S_o} + {h \over R} $

$ \sin \theta_2 \approx \sin b - \sin c \approx {h \over R} - {h \over S_i} $

$ {n \over S_o} + {n' \over S_i} = {(n'\ - n)\over R} $

Note that

• $ S_i $ does not depend on the angle $ a $.
• Light coming from a point on the filament passes through a point after refraction.

a) $ S_o > {n\ R \over (n'\ - n)}\ \Rightarrow S_i > 0 $ ,	b) $ S_o = {n\ R \over (n'\ - n)}\ \Rightarrow S_i \to + \infty $,	c) $ S_o = {n\ R \over (n'\ - n)}\ \Rightarrow S_i < 0 $

Lenses

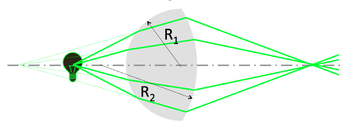
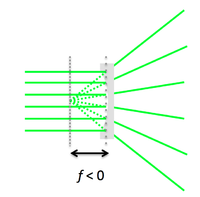
Lens maker formula

A simple lens consists of two spherical interfaces of radii of curvature $ R_1 $ and $ R_2 $. Its focal length $ f $ is given by the lens maker formula:

$ {1 \over S_o} + {1 \over S_i} = {1 \over f} = {(n'\ - n) \over n} \left ( {1 \over R_1} - {1 \over R_2} \right ) $

Bi-convex lens	Plano-concave lens

• In your ray-tracing studies, you'll use the image from the first refraction as the object for the second.
• Note the sign convention for the second surface: $ R_2 $ < 0 for a convex lens, and $ (n'\ - n) $ has opposite sign.
• Concave lens: the lens maker formula holds for $ R_1 $ < 0.

Types of spherical lenses

To minimize spherical aberrations, the general rule is to position the curved side of the lens toward the collimated/straight light.

Ray Tracing

Principles

	Rays passing through the optical center of a lens continue in a straight line
	Rays traveling parallel to the optical axis pass through the focal point after refraction and vice versa
	Parallel rays pass through the same point in the focal plane after refraction and vice versa

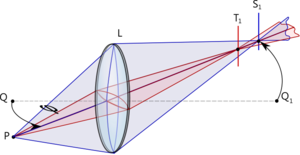
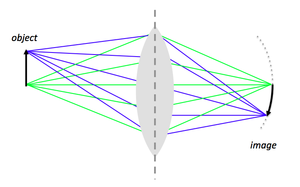
Objects and images

Imaging with a lens

Imagine the object is made up of many point sources. After refraction, all the rays from a single point in the object plane reach the same location in the image plane. This forms a real, inverted image.

Magnification

By similar triangles, magnification is equal to the ratio of distances to the lens:

$ M = {h_i \over h_o} = {S_i \over S_o} $

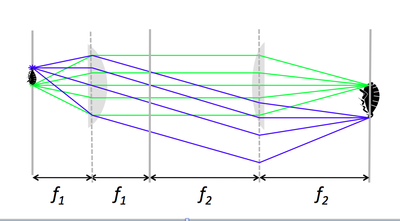
A 4 f or compound microscope

• A 4 f microscope is made of two positive lenses, placed at the sum of their focal lengths apart.
• An object (sample) placed in the focal plane of the first lens gets magnified by the ratio of focal lengths, $ f_2 / f_1 $.

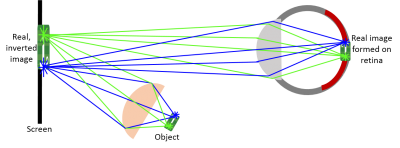
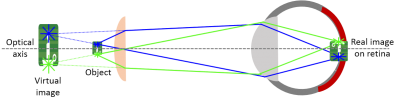
The eye as a lens

	The eye’s optical system focuses the light from each point of the object on to a point on the retina to create an image.
	When an image is projected on a screen, the projection system focuses the light from each point in the object to a corresponding point on the screen. When you view this real image, your eye focuses the light from each point on to your retina – just like it would if the object was located on the screen. (Hence, the convincing illusion.)
	You can also view a real image directly. In an optical system the image of a lens acts like the object of the next.
	You can observe a virtual image. In the virtual image, each light ray from a point on the object appears to originate from a different point in space. Unlike a real image, you cannot position a screen to show the image – there is no place that the rays come together, unless they are refracted by another lens (your eye, in this case). The image in a magnifying glass is virtual.

Aperture and field stops

Aperture stop and image brightness

• The aperture stop of an imaging system is the optical element that limits angle of rays passing through the system from a source on the optical axis.
• For an off-axis object, the chief ray is the ray that passes through the center of the aperture stop, and the marginal rays are those that pass through the edge of the aperture stop.
• The size of the aperture stop determines the light-gathering capability of an instrument, and thus the brightness (or irradiance in W/m²) of its images.
• Typically in a microscope, the aperture stop will be the objective lens.

The aperture stop in system can be (top) the left diaphragm, (middle) the first, left lens, or (bottom) the second, right lens.

Light-gathering power of oil-immersion and air-immersion lens, showing that $ \alpha_{oil} > \alpha_{air} $.

Numerical aperture

• The numerical aperture (NA) is another important measure that characterizes the light-gathering power of a lens.

$ NA = n\ \sin \alpha $

where $ n $ is the index of refraction of the medium between the object (sample) and the lens and $ \alpha $ is the half-angle defined by the limiting ray.

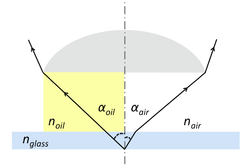
• An oil-immersion objective lens will thus have a greater NA than an air-immersion objective lens ($ n_{oil} > n_{air} $ and $ \alpha_{oil} > \alpha_{air} $; indeed, little refraction occurs at the glass-oil interface where $ n_{oil} \approx n_{glass} $).

Field stop and field of view

• The field stop is the optical element that blocks off-axis rays passing through the center of the center of the aperture stop (i.e. the chief rays).
• The field stop determines how much of the object can be viewed, in other words: the field of view of the imaging system.
• In your 20.309 microscope, the field stop will be the CCD camera.
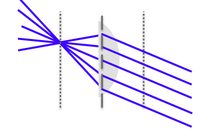
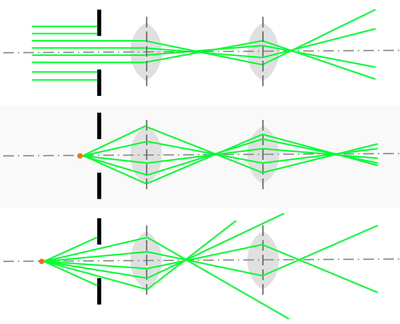
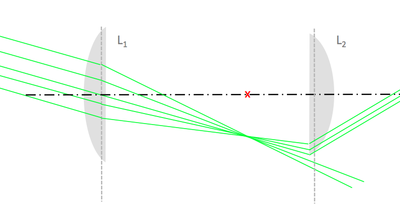
• A finite-size lens can also act as a field stop. Below is an illustration of this vignetting effect: a cone of light rays from an off-axis object is not transmitted in its entirety, but rather partially cut off by the field stop of the system, L₂'s rim.

Optical aberrations

In practice, as the polychromatic nature of white light is taken into consideration, and as imaging conditions depart from the Gaussian optics approximations that have framed our representations so far, optical aberrations get introduced into images formed by lenses. Aberrations fall into two main categories: aberrations caused by wavelength variations (chromatic), and aberrations caused by the lens's spherical construction (these are known as Seidel's aberrations: spherical, coma, astigmatism, field curvature, and distortion) .

From fsu.edu Axial chromatic aberration and achromat doublet correction

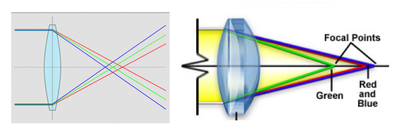
Chromatic aberrations

• Axial chromatic aberration is due to dispersion by the lens's medium whose index of refraction effectively varies with the light wavelength: the blue part of the spectrum is refracted to a greater extent than the red portion.
• Lateral chromatic aberration manifests itself by a difference in magnification of blue vs. red images of white-light-illuminated objects, which causes color ringing at the outer regions of the field of view.
• An achromatic doublet combination (the association of a converging lens with a weaker diverging lens) can correct chromatic aberrations for certain wavelengths.

Longitudinal and transverse spherical aberrations

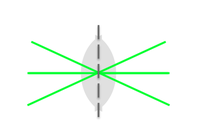
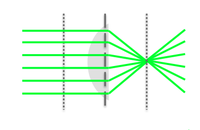
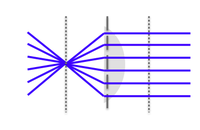
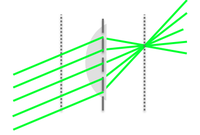
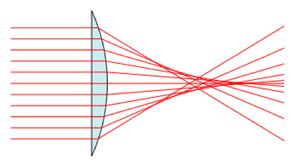
Spherical aberrations

• Peripheral rays and axial rays have different focal points, because the former are actually refracted to a greater degree than the latter.
• Spherical aberrations arise from the higher-than-first-order terms in the sin θ and cos θ expansions that become non-negligible as the incident light angle θ increases.
• Spherical aberration causes the image to appear hazy or blurred and slightly out of focus.
• This effect significantly degrades the resolution of the lens because it affects the coincident imaging of points on and off the optical axis.

In coma and astigmatism, parallel off-axis oblique rays do not focus at one point in the image plane, but rather at distinct point in the sagittal and meridional planes, causing image distortion.

Coma and astigmatism

• Comatic aberration results in off-axis point objects appearing asymmetrical and taking a comet-like shape. Comatic aberration is most commonly encountered when a microscope is out of alignment.
• Astigmatism engender ellipses or blurred lines as images of speciment points. Depending on the angle of the off-axis rays entering the lens, the line image may be oriented either tangentially or radially.

Petzval distortion results in image curvature.

Petzval distortion or field curvature

• Instead of generating image points of a flat object onto a flat screen as we have idealized so far in ray tracing estimations, a simple lens

focuses these image points onto a spherical surface, shaped as a curved bowl whose curvature, the Petzval curvature, is the reciprocal of the lens radius.

Lab manual homepage

Lab Manual: Optical Microscopy

References