Lab Manual: Optical Microscopy
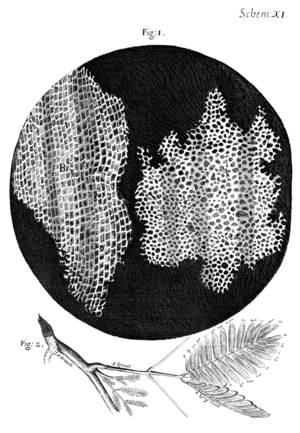
I took a good clear piece of Cork, and with a Pen-knife sharpen'd as keen as a Razor, I cut a piece of it off, and thereby left the surface of it exceeding smooth, then examining it very diligently with a Microscope, me thought I could perceive it to appear a little porous; but I could not so plainly distinguish them, as to be sure that they were pores, much less what Figure they were of: But judging from the lightness and yielding quality of the Cork, that certainly the texture could not be so curious, but that possibly, if I could use some further diligence, I might find it to be discernable with a Microscope, I with the same sharp Penknife, cut off from the former smooth surface an exceeding thin piece of it, and placing it on a black object Plate, because it was it self a white body, and casting the light on it with a deep plano-convex Glass, I could exceeding plainly perceive it to be all perforated and porous, much like a Honey-comb, but that the pores of it were not regular; yet it was not unlike a Honey-comb in these particulars.
I told several lines of these pores, and found that there were usually about threescore of these small Cells placed end-ways in the eighteenth part of an Inch in length, whence I concluded there must be neer eleven hundred of them, or somewhat more then a thousand in the length of an Inch, and therefore in a square Inch above a Million, or 1166400. and in a Cubick Inch, above twelve hundred Millions, or 1259712000. a thing almost incredible, did not our Microscope assure us of it by ocular demonstration.
— Robert Hooke from Micrographia: or Some Physiological Descriptions of Minute Bodies made by Magnifying Glasses with Observations and Inquiries Thereupon (1665)[1]
Introduction
In this lab, you will build an optical microscope using lenses, mirrors, filters, optical mounts, CCD cameras, lasers, and other components in the lab. The work is divided into 3 parts. Each part requires some lab work, some analysis, lots of clear thinking, and a written report. You will submit a short, group report after parts 1 and 2. The final report should include results from all 3 parts of the lab. You may revise and improve your part 1-2 reports before the final submission.
Part 1
In part 1 of the lab, you will build a compound microscope, determine its magnification, and attempt to measure the size of microscopic objects. The instrument you create will have a great deal in common with the microscope Robert Hooke built in the mid-1660s. Hooke meticulously documented his microscopic observations and published them in a popular volume called Micrographia in 1665. The measurements you make in part 1 will call to mind Hooke's early quantification of the size of plant cells (see quote at top of page). You will grapple with many of the same challenges Hooke faced: resolution, contrast, field of view, optical aberrations, and obscurity of thick samples. (To overcome the thick sample problem, Hooke used a very sharp knife to cut an "exceeding thin" slice of cork — a technique still in everyday use.)
Hooke spent countless hours hand drawing the breathtaking illustrations for Micrographia. A CCD camera in the image plane of your microscope will provide a huge advantage. You will be able to record micrographs nearly as spectacular as Hooke's in a fraction of a second and with far less skill. (As a young man, Hooke apprenticed as a painter. The guy could draw.)
Specimens in part 1 will be illuminated by an LED that shines light through the sample plane. The illumination will show up as a bright background in your images. The unsurprising name of this method is: transilluminated, bright field microscopy. Transillumination works well for samples that absorb or scatter a lot of light. Most biological samples have low contrast when imaged this way. Despite the limitations of bright field microscopy, many important discoveries were made with this simple method. Hooke was an early discoverer of plant cells, but he was mostly interested in how the cell structure of his cork sample explained the material's unique mechanical properties. He soon trained his microscope on other things (like glass canes, a bloodsucking louse, and feathers).
Likely inspired by Micrographia, a Dutch draper named Anton van Leeuwenhoek honed his lens-making skills and developed his own microscope. Van Leeuwenhoek was intensely interested in the tiny creatures he dubbed "animalcules" that he observed in water, blood, semen, and other specimens. Looking at samples of plaque from his own mouth, van Leeuwenhoek recorded: "I then most always saw, with great wonder, that in the said matter there were many very little living animalcules, very prettily a-moving. The biggest sort. . . had a very strong and swift motion, and shot through the water (or spittle) like a pike does through the water. Looking at the second sort. . . oft-times spun round like a top. . . and these were far more in number." (Sadly, the colorful term "animalcule" did not have as much staying power as "cell.") Van Leeuwenhoek discovered bacteria, protozoa, spermatozoa, rotifers, Hydra, Volvox, and parthenogenesis in aphids. He was truly the first microbiologist.
Perhaps the most remarkable discovery ever made with nothing but a simple light microscope was genetic transposition. Barbara McClintock was a talented microscopist who developed a technique that enabled her to distinguish individual chromosomes in Zea mays (corn) plant cells. One important element of her method was that she prepared her samples by squashing them instead of cutting thin slices as Hooke did 300 years earlier. She observed genetic transposition through an optical microscope in 1944, nearly 10 years before the chemical structure of DNA was deciphered. Several decades elapsed before molecular techniques sufficiently sophisticated to confirm her discovery were developed.[2] McClintock was awarded the Nobel Prize in Physiology or Medicine in 1983 for her discovery.
An example microscope made by the instructors will be available in the lab for you to examine. Feel free to make improvements on this design. Mechanical stability will be crucial for the particle tracking experiments in parts 3 and 4 of the lab. The required stability specification will be achieved through good design and careful construction — not by indiscriminate over-tightening of screws.
Part 2
The development of fluorescence microscopy has been the single most important rejoinder to the contrast problem (and more recently to the resolution problem). Fluorescence microscopes rely on special molecules in the sample called fluorophores that absorb photons of one wavelength and then turn around and emit photons of a longer wavelength. Optical filters separate excitation from emission, producing an image that shows only the cordial glow of the fluorescent molecules on a dark background. Filtering out the illumination provides much better contrast than transillumination. Excellent techniques exist for attaching fluorophores to molecules of interest. The three principal techniques are: fluorescent stains, immunofluorescence, and fluorescent proteins. Fluorescent stains such as DAPI are small molecules that bind to particular sites (the minor groove of DNA in the case of DAPI). Immunofluorescence exploits antibodies conjugated to fluorophores to label specific molecules. A dizzying array of antibodies and dyes exists. Because they are amenable to genetic manipulations, fluorescent protein techniques have had perhaps the most profound impact on biological science. The 2008 Nobel Prize honored Osamu Shimomura, Martin Chalfie and Roger Tsien for developing the green fluorescent protein (GFP).
In part 2 of the lab, you will augment your microscope to support fluorescence imaging. To test the new capabilities of your microscope, you will image fluorescent microspheres and immunofluorescently labeled biological samples. You will use image processing techniques to correct the images for nonuniform illumination.
Part 3
In part 3, you will make quantitative measurements using fluorescence. You will image tiny, fluorescent microscpheres to measure the resolution of your microscope. The beads are so small they act essentially like point sources. You will also take movies of larger microspheres diffusing in solvents of different viscosities. You will use image processing and particle tracking techniques to measure the diffusion coefficient of the particles and estimate the viscosity of the solvents. The details of some of the solvents will be revealed to you and others will be unknown.
Then, you will use particle tracking to make quantitative measurements of a biological sample. Procedures vary from year to year. Details will be provided in class.
The final report should consist of all 3 sections in a single file. In the final document, you may revise any part of the first two sections without penalty. Only the final report will be graded. You may not skip any of the intermediate reports.
Follow the format suggested in the Microscopy report outline.
Background materials and references
The following online materials provide useful background for this part of the microscopy lab.
- Geometrical optics and ray tracing
- Physical optics and resolution
- Lectures 1 through 9 of the 20.309 class
- From Nikon MicroscopyU
- Conjugate planes in optical microscopy (includes transmitted and reflected (epi) illumination)
- Snell's law
- Resolution
Microscope design
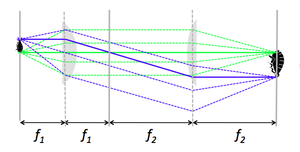
The diagram on the right shows a microscope that consists of two, positive focal length lenses of focal lengths f1 and f2, with f1<f2. The lens nearer to the object is called the objective lens. The lens closer to the image is called the tube lens — presumably because it resides inside the tube of an old fashioned microscope. The distance between the lenses is equal to the sum of their focal lengths, f1+f2.
In this type of microscope, objects such as bloodsucking lice are placed a distance f1 from the objective lens. The diagram shows rays emanating from two representative points on the object in blue and green. Optical ray tracing rules dictate that rays emerging from a single point in the focal plane of a lens are parallel or collimated after refraction. “Collimate” is a term frequently used in optics that means, “to make parallel.” Thus, all of the rays originating from a single point on the sample travel in parallel in the space between the two lenses.
The same ray tracing rule can be applied in reverse to ascertain what happens when a set of parallel rays strikes the tube lens. After refraction, parallel rays pass through a single point in the back focal plane of the tube lens. This forms an image at a distance of f2 from the tube lens. You can verify by similar triangles that the magnification of the system is -f2/f1, minus one times the ratio of the focal lengths of the lenses. (The sign is negative because the image is inverted.) The total length of the system from object to image is 2f1+2f2. Based on this observation, somebody decided that it would be clever to call this design a "4f" microscope, in spite of the fact that there are two different efs. It's no wonder that many people find engineers a bit curious. They are meticulous about some terms and remiss about others. Feel free to call it a 2f1+2f2 ‘scope in your head.
The microscope you build in this lab will be a 4f system, assuming you follow instructions reasonably well.
Objective lenses
To make a microscope with high magnification and a lot of light gathering capacity, it is desirable to use an objective lens that has a large cross section and a short focal length. Unfortunately, simple lenses with these attributes exhibit terrible aberrations. (Hooke used a small ball of glass as his objective lens. It is a wonder that he was able to produce such detailed and accurate drawings from the distorted field of view he observed. It is likely that Hooke was a more patient person than you.) To reduce aberrations to an acceptable level, modern objective lenses consist of many optical elements in series.
Despite the complexity (and added thickness) of all of the lenses inside modern objectives, the way they bend light is almost exactly the same as a single, simple lens with a spatial rift in the middle. Yes, I mean the hoakey, Star Trek sort of spatial rift where one bit of space connects to another, discontiguous bit of space — perhaps resulting from a transporter malfunction during a tachyon burst that hit chroniton beam at the entrance of a wormhole.
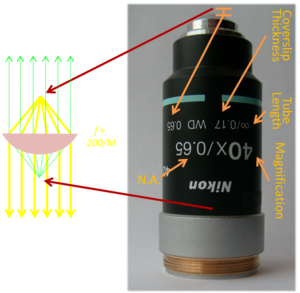
As shown in the diagram, there is a special point on the optical axis in front of the objective that is analogous to the front focal point of a simple lens. Just like a simple lens, a point source at that location results in collimated rays propagating parallel to the optical axis out of the back end of the objective (yellow rays in the diagram). The manufacturer specifies the special point as a distance in millimeters in from the frontmost optic of the objective, called the working distance. The working distance is printed on the side of most objectives after the letters “WD.”
On the other side of the objective, there is another point that corresponds to the back focus of a simple lens (green rays in the diagram). The location of that point varies as a function of the magnification of the objective. For high magnification objectives, the point is inside the barrel of the objective. It may be outside the objective for low power objectives. Regrettably, the manufacturer does not specify this distance.
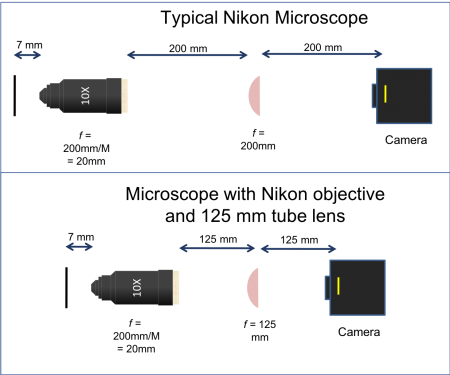
Except for the spatial rift, it is nearly always safe to imagine that a complicated objective lens functions like a single, simple lens of a certain focal length. The analogous focal length is called the equivalent focal length, or EFL. You can find the EFL of an objective lens by the formula EFL=RTL/M, where RTL is a mysterious quantity called the reference tube length and M is the magnification. M is printed on the side of the objective in a large font, usually followed by an “x.” RTL is a manufacturer-specific number that is not printed on the objective, or just about anywhere else. RTL is equal to the focal length of the tube lens embedded inside the microscope that the manufacturer wants to sell you. Since we are building our own microscope, we will have to figure out what sort of tube lens the manufacturer had in mind. The objectives you will use were made by Nikon, which means that they were probably designed for a 200 mm tube lens. Thus, for a Nikon objective, EFL=200 mm/M. A 40x Nikon objective acts like an f=5 mm lens (with a spatial rift of perhaps 30 mm).
The objective's numerical aperture, or NA, is printed on the objective after the magnification and a slash (40x/0.65, for example). NA is a measure of the light gathering capacity. More is better.
The infinity symbol near the silver ring on the objective in the picture specifies the tube length. This is different than the RTL from before. The tube length is the distance in millimeters at which the objective is designed to form an image. Older objectives often have a finite tube length like 160 or 200. Lenses with a finite tube length are optimized for a slightly different optical design in which the sample plane is a bit farther away than the front focus and the objective forms a real image. An infinity symbol in this location indicates that the objective is designed to have the sample exactly in its front focal plane in order to produce collimated light. Infinity corrected objectives are intended to be used in a way that they do not form an image.
The number after the ∞/ is the coverslip thickness. Aberrations in the objective are optimized for a specific type of coverslip. Some very fancy objectives have an adjustment ring that allows for different thicknesses.
Other markings you'll find on objectives include an intricate yet arcane nomenclature and set of acronyms that describe its optical properties. This excellent webpage has a good explanation of the markings.
A simple microscope made with a 10x Nikon objective is shown on the right. The working distance of the objective is 7 mm. As per the manufacturer's specification, an f=200 mm tube lens is placed 200 mm from the objective. The tube lens forms an image at a distance of 200 mm.
To record images, a CCD camera is placed in the image plane. The CCD camera is essentially a grid of light detectors connected to a computer. Each detector or pixel measures 7.4x7.4 microns. The camera you will use has a rectangular array of 656x492 of pixels.
Lenses
Plano-convex spherical lenses are available with focal lengths of 25, 50, 75, 100, 125, 150, 175, 200, and 250 mm. Plano-concave lenses with focal lengths of -30, -50, and -75 are also available. It is acceptable to mount a lens between the end of a tube and a tube ring or between two tube rings. To facilitate easy installation and removal, mount lenses in short (e.g. 0.5") lens tubes. In most cases, the convex side of the lens faces toward the collimated beam. The flat side goes toward the convergent rays.
Microscope design
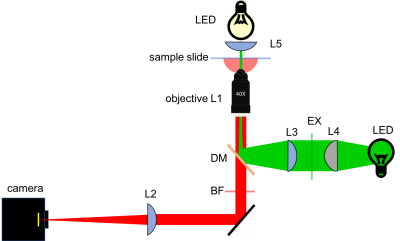
There are a few additional things to keep in mind as you design your microscope. In traditional microscopes, the objective is above the sample and the observer looks down through an eyepiece. This is not a good arrangement for many biological applications. Looking through the growth medium in a petri dish or well distorts the image, so you would prefer to observe from the same side the cells are growing on. If you turn the dish upside down, all of to goo runs out on to the microscope stage. To solve this, biological microscopes usually place the objective underneath the sample. (This also explains why the print on the objective is upside down.) The optical path is pretty long, almost half a meter. It would be inconvenient to lie on the floor while making observations or stand on a ladder while changing samples, so most inverted microscopes use a 45 degree mirror, like M1 in the diagram below, to redirect light sideways.
You are going to add fluorescence capability to your microscope in part 2. With a little bit of planning, you can build your part 1 ‘scope in such a way that you won't have to take your instrument apart for part 2. One of the key components needed for epifluorescence is a dichroic mirror, DM in the diagram. Dichroic mirrors reflect some colors of light, but pass others. The one you will use reflects the green laser light used to excite the sample but passes red light emitted by fluorescent molecules in the sample.
The dichroic mirror is imperfect and still allows a substantial amount of green light to pass. It is thus supplemented by a barrier filter BF to attenuate green light by 5 orders of magnitude. The combination DM + BF is essential for making good images.
In contrast with the transillumination bright-field approach where the LED incident light traverses the sample before reaching all image-forming optics, illumination for epi-fluorescence microscopy reaches the sample through the objective lens — from the same side of the sample that is observed. The rationale behind this design choice is the relative dimness of the fluorescence emission signal with respect to the needed excitation intensity. Even though fluorescence excitation and emission occur at distinct wavelengths and can thus be filtered away from one another, it is still advantageous to restrict to the utmost the amount of excitation light in the image plane.
In epi-fluorescence mode, the sample is illuminated by a green laser. Traveling through and focused by the objective lens, this collimated laser beam would result in single point illumination of the sample. To restore collimated excitation of a broader region of the sample, lens L5 must be inserted in the optical path... with the drawback that the laser beam's diameter, ~ 1.1 mm originally, thus becomes "minified" by a factor f5 / fobj, which would result in the illumination of a disc only ~ 25 μm in diameter!
A Gallilean beam expander (L3 and L4) is thus the final requirement of the microscope design. It allows the collimated laser illumination to match the CCD camera field of view. The focal lengths chosen for L3 and L4, and thus the expansion factor of the beam expander, are a tradeoff between uniformity and brightness of illumination, given the Gaussian shape of the laser beam.
Optical microscopy lab
Code examples and simulations
- Converting Gaussian fit to Rayleigh resolution
- MATLAB: Estimating resolution from a PSF slide image
- Matlab: Scalebars
- Calculating MSD and Diffusion Coefficients
Background reading
- Geometrical optics and ray tracing
- Physical optics and resolution
- Optical aberrations
- Aperture and field stops
- Optical detectors, noise, and the limit of detection
- Manta G032 camera measurements
- Understanding log plots
References
- ↑ Hooke, R. Micrographia: or Some Physiological Descriptions of Minute Bodies made by Magnifying Glasses with Observations and Inquiries Thereupon London:Jo. Martyn, and Ja. Allestry, Printers to the Royal Society; 1665
- ↑ See, for example: McClintock, B. The origin and behavior of mutable loci in maize. PNAS. 1950; 36:344-355. [1], [2], and Endersby, Jim. A Guinea Pig's History of Biology. Cambridge, Massachusetts: Harvard University Press; 2007.
- ↑ See class stellar site for protocol. Oh & Yamaguchi, unpublished lab report