Understanding log plots
Log plots pop up in 20.309 surprisingly frequently. The goal of this page is to help you get familiar enough with log plots so that you can easily interpret and sketch functions on a log scale.
Basics
Remember the definition of a logarithm:
- If $ y = 10^a $, then $ \log_{10} y = a $
And some of its useful properties:
- $ \log(a\times b) = \log(a) + \log(b) $
- $ \log(a^c) = c \times \log(a) $
MATLAB log function
When you see the function $ \log $ written with no base, the implied value of the base is almost always assumed to be 10 ($ \log_{10} $). There is one important exception: MATLAB. Unfortunately, the Vice President of Inconsistency and Obfuscation at Mathworks got to decide the names of the log functions in MATLAB. The MATLAB function log() returns the natural logarithm ($ \ln $) of its argument instead of $ \log_{10} $. This is just downright lame and confusing. The MATLAB function log10() returns log base 10 ($ \log_{10} $). Mail your complaints to [/dev/null].
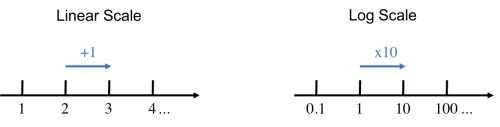
Linear vs. log scale
On a linear scale (the scale you're familiar with), moving a fixed distance along an axis is equivalent to adding a fixed number to your starting point. On a log scale, moving a fixed distance along an axis is equivalent to multiplying the starting point by a fixed number.
If you’d like to get a more in-depth explanation of the log scale Khan Academy has a nice ~11 minute video on the subject.
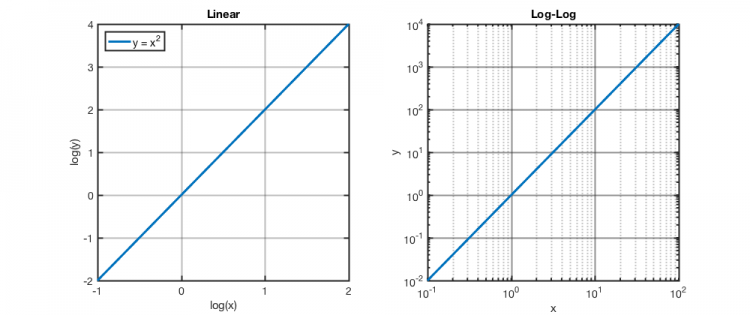
There are two ways to make a log-log plot in MATLAB. The first is to use the plot command to plot log(y) vs. log(x) on a linear scale.
plot( log10(x), log10(y))
Alternatively, you can use the loglog command to make a plot with log-scale axes:
loglog( x, y)
These two examples are compared below. The nice thing about using the second method is that you can easily read of the x and y values directly instead of having to do math in your head. And we all know how much BE students love to do math in their heads! Typically, each tick mark represents an integer times its factor of 10. So, for example, the tick to the right of $ 10^1 $ on the x-axis represents $ 2\times 10^1 $, the next is $ 3\times 10^1, $ and so on.
Use whichever method produces the clearest plot. This is normally the loglog function, but there are some times when the other format is clearer.
Note that sometimes it is more clear to plot only one variable on a log scale. The matlab commands to plot only x or y on a log scale are, respectively:
semilogx( x, y) semilogy( x, y)
Plotting power laws
So, what happens when you plot things on a log scale? Well, in general, small things get stretched and big things get squished. Not all functions are easy to translate from linear to log, but the power law is. Thankfully this is a function that comes up frequently, so let’s look at it in detail.
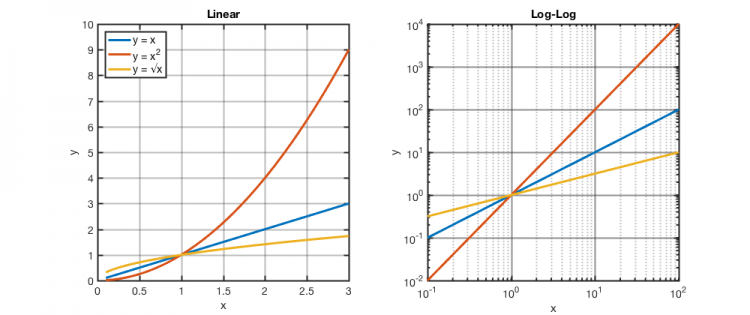
A power law is any function of the form $ y = x^n $, where $ n $ is some constant. Here are a few familiar examples for $ n= $1, 2, and 0.5 plotted on a typical (linear) scale and on a log-log plot.
Clearly, the power law looks like a straight line on the log scale. Remember that $ \log( x^n) = n\times \log(x) $, so plotting log(y) vs. log(x) is a line with a slope of n. We typically say that “it is linear on a log scale”. When we refer to the ‘slope’ of this line, we are talking about the apparent slope of the line on the log log plot. I.e. how many major grid lines do you cross in y when you increase in x by a single major grid line? For example, for $ y = x^2 $, when x goes from 1 to 10, y increases by a factor of 100 - or by 2 grid lines, so we’d say the log-log plot of $ x^2 $ has a slope = 2.
What if we ask you to sketch a function that has a power law behavior? You now know that the slope of this line would be equal to the power (n), but to plot a line you need one more piece of information. You must choose a point through which the line passes. You are free to choose any point you want, but it can sometimes be convenient to choose the point $ x= 10^0 = 1 $. (I’ll let you think about why x = 0 would be a poor choice.) In the above case, conveniently, when x = 1 all functions have y = 1, so they all pass the same point. Now you have all you need. Give it a try on your own with $ x^3 $.
An important observation we can make from the above comparison is that you can plot a huge range of values on a log plot. On the linear scale, the range of x values we plotted was only 0 to 3. If we were to plot a larger range of x values, the functions $ y = x $, or $ y = \sqrt{x} $ would get squished down into the x-axis because $ x^2 >> x $ for large x. But on the log scale, you can clearly compare all functions from a huge range (in this case x = 0.1 to 100).
Multiplying by a constant
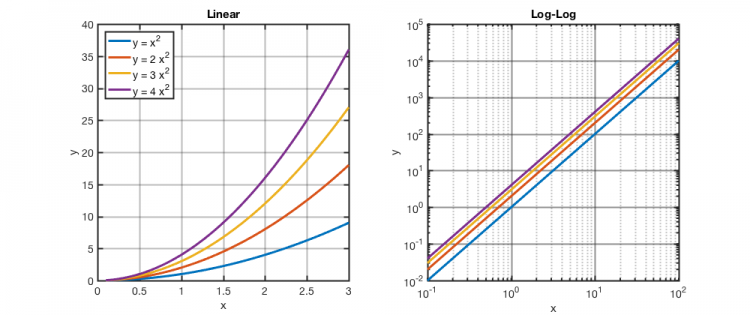
What happens if you multiply a function by a constant on a log scale? Looking at the math: if $ y = a\times f(x) $, then $ \log(y) = \log(a)+ \log(f(x)) $. In other words, the plot will have the same shape as $ \log(f(x)) $ but will be shifted up by a constant offset $ \log(a) $.
Here’s the plot for the case where $ y = a\times x^2 $:
Adding a constant
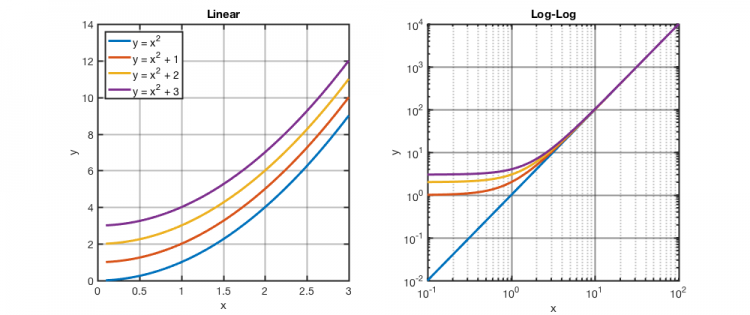
If we add a constant to a function, there is no convenient log property that we can rely on to simplify the expression $ \log(a+f(x)) $. Let’s just see what happens to the plot when add different constants to $ x^2 $:
Interesting: the function is unchanged when x is large, but then asymptotes to different values for small x.
This brings us to another useful property of log plots. They highlight limiting behavior of a function. In the above case for $ y = a + x^2 $, when $ x^2<<a $, then $ y\approx a $, but when $ x^2>>a, y\approx x^2 $. We can then easily sketch any function by connecting the limiting behaviors.
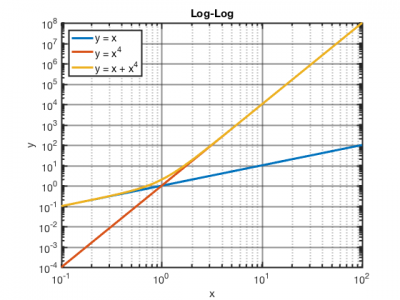
Let’s try plotting the function $ y = x + x^4 $. When $ x <1 , x >> x^4 $, so $ y \approx x $. But for $ x>1 $, $ x <<x^4 $ so that $ y\approx x^4 $. To sketch this function on a log-log plot, start by sketching the two lines for $ y = x $ and $ y = x^4 $ (check out the blue and red lines on the plot below). Now to sketch the overall function, you just need to connect the limiting behavior (yellow line). Notice that the two lines approximate the original function very well, except for a small region around the ‘corner’ where they meet. If you're sketching this function by hand, it's ok to approximate what's going on in the corner region, as long as you have the right limiting behavior.
Summary
Hopefully this page has refreshed your memory on logarithms and log scales. If you'd like more practice I would recommend firing up MATLAB and plotting a variety of functions on both log and linear scales. Although they can be counterintuitive at first, with practice they will actually become useful tools in your data visualization arsenal.
A few key takeaways:
- Log plots are useful when you want to emphasize the limiting behavior of functions, or compare several functions over a large range of values
- Power laws are linear on a log scale, with a slope equal to their exponent
- Multiplying a function by a constant looks like adding a constant offset on a log-log plot
- To plot a function with multiple powers of x, first plot the limiting behavior, then approximate the connecting regions.