Spring 2020 Assignment 7
Measuring action potentials
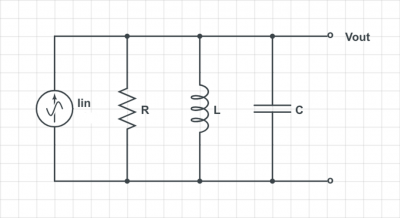
The patch clamp is a technique for measuring voltages produced by electrically active cells such as neurons. One potential problem with the patch clamp technique is that a device must be physically attached to the neuron being measured. Connecting anything to a neuron might alter its behavior. The measurement device itself can distort the signal. This problem of loading the system to be measured affects many kinds of measurements (not just electronic ones). In this problem you will consider a simple model of the distortion in a patch clamp measurement.
A simple equivalent circuit model for a neuron consists of a time-varying voltage source in series with an output impedance of 1011 Ω. There is an oscilloscope next to the neuron with an input impedance of 106 Ω and an input capacitance of 20 pFd. A new UROP in the lab attempts to measure electrical spikes produced by a neuron (called action potentials) by connecting the patch clamp apparatus to the oscilloscope with a 6 meter cable that has a capacitance of 80 pFd. Action potentials are about 100 mV in amplitude and about 1 ms in duration. You can model the noise in the system as a random, additive, normally distributed voltage with a standard deviation of 10-3 V.
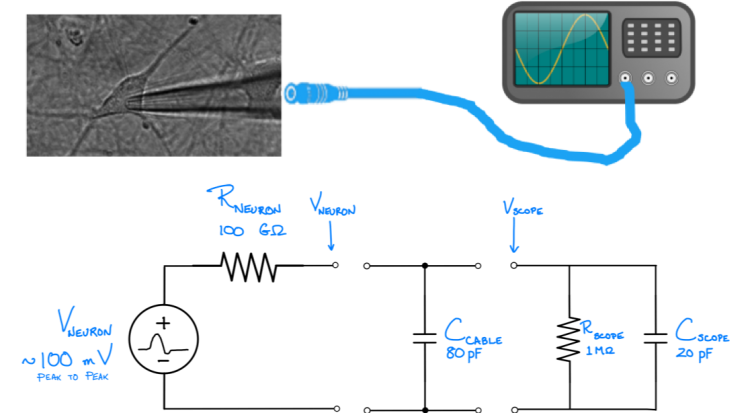
Easy Bode plots
| 1 | 2 |
|---|---|
|
|
| 3 | 4 |
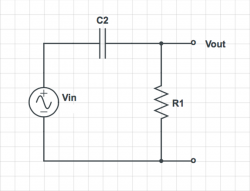
|
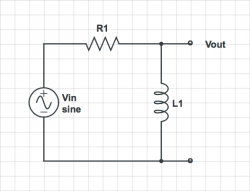
|
Harder Bode plots
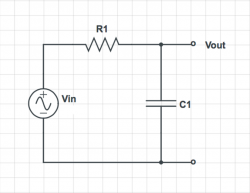
{{Template:Assignment Turn In|message= For each of the circuits below, find the transfer function $ H(\omega)=\frac{V_{out}}{V_{in}} $.
Simplify the transfer functions using the following assumptions:
- For the first circuit, assume that $ R_1 C_1 \ll R_2 C_2 $, and $ R_2 \gg R_1 $
- For the second circuit, assume that $ R_1 C_1 = R_2 C_2 $, and $ R_2 \gg R_1 $
On a log-log plot, sketch the magnitude of the simplified transfer function versus frequency. Label cutoff frequencies. Sketch the phase angle of the transfer function versus frequency on a semi-log plot. Suggest a descriptive name for each circuit.
| 1 | 2 |
|---|---|
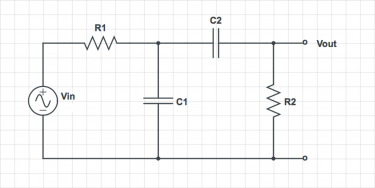
|
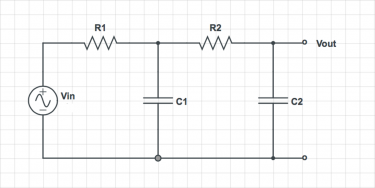
|
Linear systems
| 1 | 2 |
|---|---|

|

|
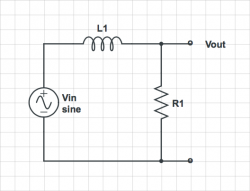
Second-order system
| |
Find the transfer function $ H(\omega)=\frac{V_{out}}{I_{in}} $ for the circuit below. |
System identification
For each of the four known and unknown frequency response measurements in the Dropbox directory, find the best-fit transfer function. Plot your results, including raw data and fit. Provide a diagram for circuit that could have generated each observed response. Include relative component values (which could be scaled by an arbitrary factor).
(The folder with the data and code is called "Frequency Response Data for Assignment 7")