Lab Manual: Limits of Detection
—Robert Hooke (1675)
Ut tensio, sic vis
—Robert Hooke De potential restitutive (1678)
The Power of any Spring is in the same proportion with the Tension thereof: That is, if one power stretch or bend it one space, two will bend it two, and three will bend it three, and so forward. Now as the Theory is very short, so the way of trying it is very easy ... it is very evident that…in every springing body…the force or power thereof to restore it self to its natural position is always proportionate to the Distance or space it is removed therefrom.
—Robert Hooke De potential restitutive (1678)
Understanding how fishes generate external fluid force to swim steadily and maneuver has proven to be difficult because water does not provide a stable platform for force measurement.
—George V. Lauder and Eliot G. Drucker (2002)
Overview
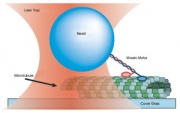
Atomic force microscopy and optical trapping are key techniques for investigating forces in biological systems at cellular and molecular levels. Both instruments can exert and measure forces on submicron-scale particles. This capability offers a unique and valuable tool for manipulating and measuring cell components at the single molecule level. For example, optical traps have been used extensively to investigate the mechanical properties of biological polymers and the force generation mechanisms of molecular motors. In many studies, optical tweezers apply force to functionalized microspheres, which act as convenient handles attached to molecules of interest.
To make quantitative force measurements, AFMs and optical traps record displacement of objects being measured versus time. For small displacements, the exerted force is very nearly proportional to displacement. The force/displacement relationship is modeled by Hooke's law: F = -αx, where α is the spring constant. The detector produces a voltage proportional to displacement. The constant of proportionality that converts voltage to distance is called the responsivity of the instrument and denoted by the letter R. Both α and R must be found through a process called calibration. Accurate force and position measurements depend on careful calibration of R and α. On the AFM, α is a function of the cantilever geometry. The optical trap's stiffness depends on trapping laser power, bead size, bead composition, and optical properties of the sample.
In this lab, you will investigate the limits of force detection using AFM and optical traps. You must attend a one-hour lab session during which an instructor will help you take data. You will analyze the data to determine α and R, and you will calculate the minimum detectable force, δ, for both instruments.
Background reading
- Neuman & Nagy. Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy. Nature Methods - 5, 491 - 505 (2008).
Measuring force
Fish are incredibly cool[1]. Many species, like the Atlantic bluefin tuna, are sleek, high-speed swimming machines with hydrodynamic lines and powerful bodies, while others like the ocean sunfish are preposterous assemblages of parts that could easily be mistaken for a square, flat boulder with fins, eyes, and comical lips glued on — or even a sea monstah[2] Because sunfishes are so ridiculous, for a long time they were thought to be weak swimmers with little control over their destinies — essentially gigantic pieces of plankton at the mercy of the tides. How could a creature with such a ludicrous swimming stroke possibly navigate the open ocean? But recent research suggests that sunfish are actually pretty good at getting where they want to go.
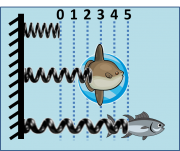
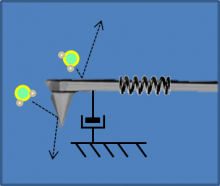
If you wanted to study how the force generated by the sunfishes' ridiculous fluttering motion compares to the powerful and athletic wriggle of the mighty tuna, you might construct an instrument like the Fish-o-Meter shown at right. One of the most common ways to measure force is to attach the force generator to a spring. The constitutive equation for deformation of a spring is $ f=-\alpha x $, where $ f $ is the force, $ \alpha $ is a constant of proportionality called the spring constant, and $ x $ is the displacement of the spring from its natural length. The negative sign indicates that a spring's restoring force acts in the opposite direction of the applied force. Even though this simple, linear model clearly does not capture all the nuances of a spring's behavior, it's a very good approximation in most cases so long as long as magnitude of the spring's deformation is smaller than a certain threshold. (The threshold depends on how the spring is made.) The Fish-o-Meter is an indirect measuring device. It exploits the spring as a force-to-distance converter. Distance can be measured directly. Force is calculated from the raw instrument reading using Hooke's law as the measurement model. The more the spring stretches, the greater the force.
Building a Fish-o-Meter would entail solving a many practical problems. First off, McMaster Carr lists thousands of springs for sale. Which one should you choose? (Maybe one of the spring assortments? Fish are all slimy and wriggly[3], so you would have to devise some clever way of attaching the fish to the spring. (It would be difficult to come up with an arrangement that didn't interfere with the fishes' swimming motion. In any case, the spring would pull back on the fish and eventually stop its motion, which might have a significant effect on its swimming.) And it would be challenging to read the Fish-o-Meter because the force generated by a swimming fish is not constant. Perhaps you could add an underwater strip chart recorder to the setup.
Force measurement model
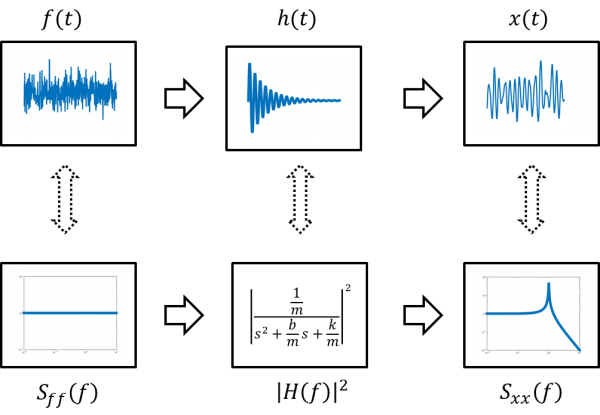
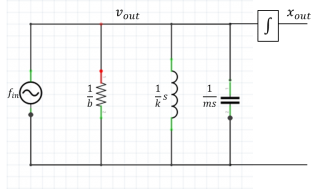
The AFM and the optical trap can both be modeled by a linear system with a mass, spring, and damper in parallel, as shown in the figure below. (The elements all have the same velocity, so they are connected in parallel.) In the AFM, the restoring forceAir or water molecules collide with the cantilever or trapped particle, which drives the system with white noise.
|
|
|
| RLC circuit model of AFM excited by collisions with air molecules. The integrator converts velocity to position. | ||
The transfer function of the circuit model is:
- $ \frac{x_{out}}{f_{in}}=\frac{\frac{1}{m}}{s^2+\frac{b}{m}s+\frac{k}{m}} $
In the time domain, random force input $ f(t) $ drives a second-order system to produce position output $ x(t) $.
The driving force has a constant power spectrum $ P_{ff}=\frac{2K_BT}{\pi^2\Beta} $. The output power spectrum $ P_{xx}(f) $ is equal to the input spectrum times the magnitude of the transfer function squared.
Optical trap procedure
The optical trap software produces four columns of tab-delimited data. The first two columns are the X- and Y-QPD voltages. Use the QPD responsivity, R, to convert the QPD voltages to position.The third and fourth columns are the X- and Y-axis sample stage readouts in Volts. To convert the voltage to position, use the responsivity of the stage, Rstage = 2.2 μm/V.
The calibration methods are summarized below:
| Method | Equation | QPD Responsivity | Stage Responsivity | Solvent Viscosity | Particle Diameter | Temperature | Technical Noise |
|---|---|---|---|---|---|---|---|
| $ R_{QPD} $ | $ R_{stage} $ | $ \eta $ | $ d $ | $ T $ | |||
| Equipartition | $ \frac{K_B T}{\langle ^{V_{qpd}}/_{R_{qpd}} \rangle ^ 2} $ | inverse square | none | none | none | linear and indirect (viscosity change) | systematic decrease |
| PSD | $ \left. {6 \pi^2 \eta d \, f_0} \right. $ | none | none | linear | linear | indirect (viscosity change) | small |
| Stokes | $ \langle \frac{3 \pi \eta d \, R_{stage} \, ^{d V_{stage}} / _{dt}} { ^{V_{qpd}}/_{R_{qpd}}} \rangle $ | inverse | linear | linear | linear | indirect (viscosity change) | none |
Report requirements
- Optical trap
- Find R for each power setting by the PSD method.
- Find α for each laser power setting by the Stokes, equipartition, and PSD method.
- Plot R versus laser power for the PSD method.
- Plot α versus laser power for all three methods.
- Calculate $ \delta_x $ and $ \delta_f $ for each laser power setting.
- AFM
- Find the photodiode responsivity R from the calibration data
- Find the lever stiffness k
- How far would the cantilever deflect if you placed a paperclip on the end?
- Calculate $ \delta_z $ and $ \delta_f $ for the AFM cantilever in air
Cite error: <ref> tags exist, but no <references/> tag was found