Assignment 8, Part 1: convolution
This is Part 1 of Assignment 8.
| |
Turn in your answers to the following questions |
- Convolution practice
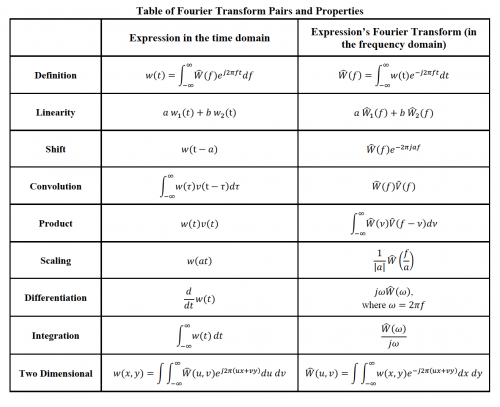
Table 8.1.1 shows plots of eight time-domain signals A-H. The table on the right includes magnitude plots of the Fourier transform of ten signals numbered 1-10. For each time domain signal A-H, write the number 1-10 in the empty column of the matching frequency-domain signal. You may use a numbered plot more than once.
Some of the frequency plots are shown on log-log axes and some are linear, as indicated by the plot title.
- DNA lab lock-in amplifier
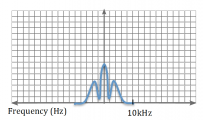
In Assignment 7, optical and electronic noise sources affected your DNA melting signal. Assume the frequency domain representation of optical and electrical noise affecting your measurement looks as in Fig. 8.1.1.
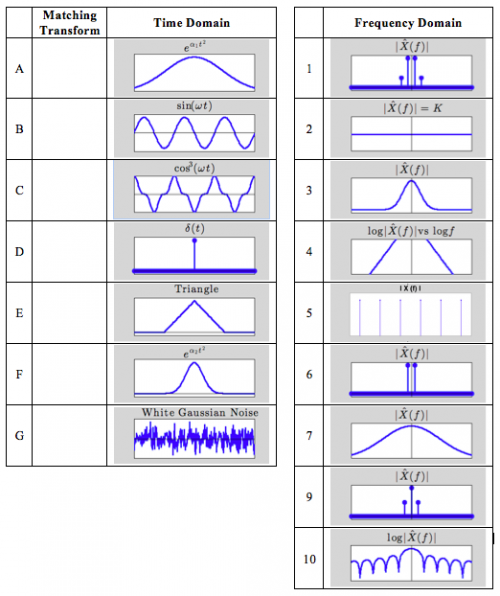
Let us also approximate the pure DNA melting signal, obtained by using constant LED illumination, as in Fig. 8.1.2 (arbitrary units on y-axes).
Since the frequency spectrum of noise in the lab overlaps with your DNA melting signal, it would be nice to reduce noise by moving the desired signal to a frequency range where the noise is at a minimum. You can do this with a lock-in amplifier, which you will implement in Part 2 of Assignment 8 in the DNA melting lab. Fig. 8.1.3 shows a schematic diagram of the lock-in amplifier.
You set your carrier frequency to 10 kHz to move your signal out of the noisy region. Draw the time and frequency domain signals at each of the four labeled points in the diagram to see how the lock-in amplifier reduces noise in your obtained signal. Label important frequencies on the frequency domain plots.
- Signal processing for nuclear magnetic resonance (NMR)
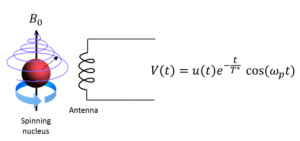
The phenomenon of NMR is the basis for many useful measurement and imaging techniques. The basic idea is to flip the spin axis of atomic nuclei in a sample that has been positioned in a uniform magnetic field using a pulse of radio waves at a particular frequency. The excitation signal must be modulated at precisely the correct frequency, ωp = γB0, called the Larmor frequency. B0 is the strength of the magnetic field and γ is the gyromagnetic ratio for the type of atom being excited. For hydrogen, γ = 42 MHz/T. The radio pulse has the effect of synchronizing the nuclear spins so that they have the same phase.
After the excitation pulse is removed, the nuclei reemit radio waves at the Larmor frequency. As the spins decohere, the emitted signal decays exponentially with time constant T*, which typically has a value around 100 ms. An antenna detects signal, as shown in the Fig. 8.1.4.- Sketch the magnitude of the Fourier transform of $ V(t) = u(t) e^{-t/T^*} cos(\omega _p t) $. You may find the Fourier transform Tables 8.1.2 and 8.1.3 useful. Indicate the approximate width of the peaks.
-
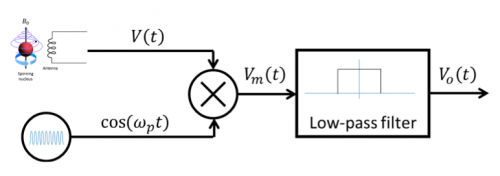
The amplitude of the NMR signal is measured by lock-in detection with a reference frequency of ωp. This means that the rapidly varying voltage from the receiver coil is multiplied by a frequency and phase matched reference signal Vr(t) and then low-pass filtered, as shown in Fig. 8.1.5.
Sketch the magnitude of the Fourier transform of the intermediate signal Vm (t) and the output signal Vo (t). What is the purpose of the low-pass filter?
- Overview
- Part 1: convolution Let's check that you're comfortable with convolution and the lock-in amplifier design;
- Part 2: lock-in amplifier
Back to 20.309 Main Page