Assignment 1, Part 2: Optics bootcamp
This is Part 2 of Assignment 1.
Lab orientation
Welcome to the '309 Lab! It's time to get your hands dirty — time to get a little mens in your manus. Step one: go to the lab. (If you are already in the lab, proceed to the next step. By the way, your hands shouldn't be dirty. That's just an expression. If your hands really are dirty, then wash them with soap and water. You are going to be handling sensitive optics!)
Before you get started, take a little time to learn your way around.
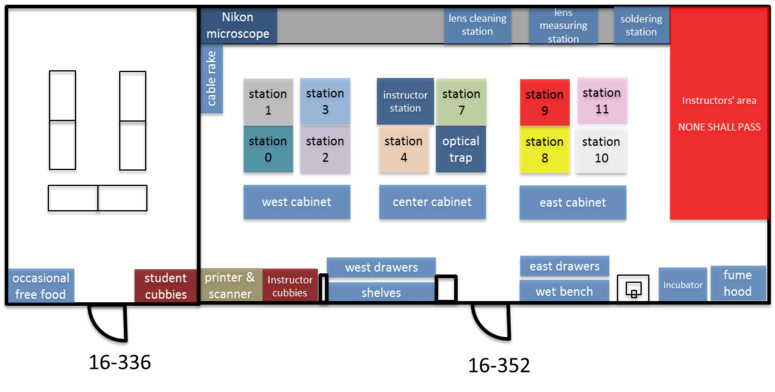
The 20.309 lab contains more than 15,000 optical, mechanical, and electronic components that you may choose from in order to complete your assignments throughout the semester. You can waste a lot of time looking for things, so take a little time to learn your way around. The floor plan below shows the layout of rooms 16-352 and 16-336. When you get to the lab, take a walk around, especially to the center cabinet, west cabinet, and west drawers. Go everywhere and check things out for a few minutes. Read the time machine poster near the printer. Discover the stunning Studley tool chest poster near the east parts cabinet.
You probably noticed that many components are filed in boxes labeled with a sequence of letters and numbers. A company called Thorlabs manufactures the most of the optics and optical mounts you will use. The lab manuals frequently refer to components by their part number, which is usually one or two letters that have a vague relationship to the name of the part, followed by a couple of numbers. For example, the Thorlabs part number for a certain type of cage plate is "CP02." Thorlabs makes many kinds of cage plates, each with a subtle variation in its design. All of the cage plate part numbers starts with the letters "CP," followed by some numbers and in some cases a letter or two at the end. The Thorlabs website has an overview page of various kinds of cage plates here. Googling "Thorlabs CP02" is a quick way to get to the catalog page for that part.
To the untrained eye, many of the components in the lab are indistinguishable. The picture on the right shows just one example of strikingly-similar-looking bits. Take care when you select components from stock. Students sometimes return components to the wrong bins. Use even more care when you put things away. It is helpful to sing the One of These Things is Not Like the Others song from Sesame Street out loud while you are putting things away to ensure that you don't make any errors. (For the final exam, you will be required to identify various components while blindfolded.)
Note that Station 9 is now the "Instructor Station," and the previously labeled instructor station is now "Station 5" and available for your use.
See! Wasn't that a worthwhile journey?
Exercise 1: measure focal length of lenses
Make your way to the lens measuring station. Measure the focal length of the four lenses marked A, B, C, and D located nearby.
| |
Report the focal length you measured for each lens A through D. |
Exercise 2: imaging with a lens
Make your way to the pre-assembled lens setup that looks like the thing on the right. You will be using similar parts to build your microscope, so take some time to look at the construction of the apparatus. Identify the illuminator, the object (a glass slide with a precision micro ruler pattern on it), the imaging lens (a, f = 35mm, biconvex lens mounted in a lens tube), and the camera (where the image will be captured). All of the components are mounted in an optical cage made out of cage rods and cage plates. The cage plates are held up by optical posts inserted into post holders that are mounted on an optical breadboard that sits on top of a vibration reducing optical table. You can adjust the positions of the object and lens by sliding them along the cage rods.
In this part of the lab, you will use this simple imaging system with one lens to compare measurements of the object distance $ S_o $, image distance $ S_i $, and magnification $ M $ with the values predicted by the lens maker's formula:
- $ {1 \over S_o} + {1 \over S_i} = {1 \over f} $
- $ M = {h_i \over h_o} = {S_i \over S_o} $
Measure stuff
- If the LED is not already on, verify that the power supply current limit is set to a number less than 0.5 A, and press the OUTPUT button. You should see red light coming from the LED.
- Move the imaging lens as close to the camera as it will go. The illuminator lens should be about 10 to 15 mm away from the LED.
- Launch MATLAB.
- The tool you will use to acquire images is implemented as a MATLAB object of type UsefulImageAcquisition. Create an instance of this type of object by typing foo = UsefulImageAcquisition() on the command line.
- The object needs to be initialized by invoking its initalize method. Do this by typing foo.Initialize(). (In MATLAB, the parentheses are optional when you invoke a method with no arguments, so you could also type just foo.Initialize. This saves a couple of characters, but it's a good idea to include the parentheses because doing so makes it clear that the statement is invoking a function and not accessing a property or something else.)
- An Image Acquisition window should appear after a little while. If it doesn't, swear at the computer a little and politely ask an instructor for assistance.
- Click Start Preview
- Configure the camera settings
- Set Gain = 0, Frame Rate = 20, Black Level = 0, and Number of Frames = 1 for now.
- Set Exposure to obtain a properly exposed image. When you have the setting right, there should be a wide range of pixel values — from dark to light — and no overexposed pixels. The histogram plot is useful for assessing the exposure setting. The horizontal axis shows all of the possible pixel values, from completely dark on the left to the brightest possible white on the right. The vertical axis indicates the number of pixels at each value. A red "X" indicates that some pixels are overexposed. (The units of the exposure setting are in microseconds.)
- You can also adjust the LED current to obtain a good exposure. DO NOT EXCEED 0.5 A.
- Move the object to produce a focused image.
- Measure the distance $ S_o $ from the target object to the lens and the distance $ S_i $ from the lens to the camera detector.
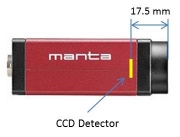
- Figure 1 shows the location of the detector inside of the camera.
- In the image acquisition window, press Acquire (lower right).
- Save your image to the MATLAB workspace
- Every time you press Acquire, the image data appears in a property of foo called ImageData. Similar to methods, use a "dot" to access properties. Note that the ImageData property gets overwritten every time you press Acquire, so you have to save the data somewhere else if you want to work with it later on.
- MATLAB has a top level context called the workspace. The workspace is a place where you can save variables and access them from the command line. Choose a descriptive variable name such as ImageSo50mm and assign it to foo.ImageData using the equals symbol: ImageSo50mm = foo.ImageData. If you'd like to see a list of the variables in the workspace, type who on the command line.
- Throughout the semester, you'll find helpful to review tips on Recording, displaying and saving images in MATLAB
- Save images in a .mat format so that you can easily reload them into Matlab for later use.
save microrulerImages % saves entire workspace to filename 'microrulerImages.mat' save microrulerImages ImageSo50mm ImageSo100mm %saves only variables ImageSo50mm and ImageSo100mm to filename 'microrulerImages.mat'
- Compute the magnification.
- One operation on images you will do frequently is to adjust their contrast. You can define a simple function that saves a bunch of typing each time you do this. MATLAB supports a feature called inline function declaration. Here is how you can define a function called StretchContrast from the command line: StretchContrast = @(ImageData) ( double( ImageData ) - min( double( ImageData(:) ) ) ) / range( double( ImageData(:) ) ). Don't sweat the details of this for now. We will talk about it in class, soon. You should only use inline function declaration to define very simple functions.
- In the MATLAB Command Window, display your image by typing figure; imshow( StretchContrast( ImageSo50mm ) );
- Go back to the command window (by pressing ALT-TAB on the keyboard or selecting it from the task bar) and type imdistline.
- Use the line to measure a feature of known size on the micro ruler
- The small tick marks are 10 μm apart
- The large tick marks are 100 μm apart
- The whole pattern is 1 mm long
- The pixel size is 6.9 μm
- Move the lens a little bit farther away from the camera and then readjust the object so that it is once again in focus. Repeat this at least 6 times. Increase the distance logarithmically — move the lens a small amount at first, and then move it larger distances as you proceed.
- In a table, record $ S_o, S_i, h_o, h_i, $, and calculate the magnification M.
- Make a plot of $ {1 \over S_i} $ as a function of $ {1 \over f} - {1 \over S_o} $, and $ {h_i \over h_o} $ as a function of $ {S_i \over S_o} $
Exercise 3: noise in images

Suppose you pointed a digital camera at a perfectly static scene where nothing at all was changing. The camera didn't move at all, the objects in the scene were perfectly stationary, and the lighting stayed exactly the same. To continue the thought experiment, say you took, oh, 100 successive pictures of the static scene at regular intervals — pretend you were entering contest to make the dullest movie ever made. In an ideal world, you would expect that every single frame of your boring movie would be exactly the same as all the others. Figure 2 depicts the structure of a dataset generated by this thought experiment as a mathematical function $ P_{x,y}[t] $. Stated mathematically, the numerical value of each pixel in all 100 of the images would be the same in every frame:
- $ P_{x,y}[t]=P_{x,y}[0] $,
where $ P_{x,y}[t] $ is the the pixel value reported by the camera of pixel $ x,y $ in the frame that was captured at time $ t $. The square braces indicate that $ P_{x,y} $ is a discrete-time function. It is only defined at certain values of time $ t=n\tau $, where $ n $ is the integer frame number and $ \tau $ is the interval between frame captures. $ \tau $ is equal to the inverse of the frame rate, which is the frequency at which the images were captured.
You have probably already guesses that, IRL, this doesn't happen. (Spoiler alert.) The 100 frames would not be identical. We will talk in class about why this is so. For now, let's just measure the phenomenon and see what we get. As long as you are in the lab, it's a pretty easy task to set up a static scene, take 100 pictures of it, and then compute how much each pixel varied over the course of the movie. Any variation in a particular pixel's value over time must be caused by noise of one kind or another. Simple enough. (An alternate way to do this experiment would be to simultaneously capture the same image in 100 identical, parallel universes. This would obviously reduce the time needed to acquire the data. You are welcome to use this alternative approach, if you like.)
Capturing an image involves measuring light intensity at numerous locations in a plane in space. The Manta G-040 CMOS cameras in the lab measure 396,032 unique locations during each exposure. Every one of those measurements is subject to noise. In this part of the lab, you will quantify the random noise in images made with the these cameras, which are the same ones that you will use in the microscopy lab.
We need a quantitative measure of noise. Variance is a good, simple metric that specifies exactly how unsteady a quantity is, so why not give that a try? (In case it's been a while, variance is defined as $ \operatorname{Var}(P)=\langle(P-\bar{P})^2\rangle $.)
So here's the plan:
- Set up a static scene that has a range of light intensities from bright to dark and point your camera at it.
- Make a movie of 100 frames.
- Compute the variance of each pixel over time.
- Make a scatter plot of each pixel's variance on the vertical axis versus its mean value on the horizontal axis, as shown in Figure 3.
Plotting the data this way will reveal how the quantity of noise depends on intensity. With zero noise, the plot would be a horizontal line on the axis. But you know that's not going to happen. How do you think the plot will look? This boring movie is getting more suspenseful all the time! I hope it doesn't have a scary ending.
Set up the scene and adjust the exposure time
- Click Start Preview.
- Configure the camera: set "Gain" to 15, "Dark Level" to 16.
- These two settings control how $ P_{x,y} $ relates to the number of photons the camera detects. In general, $ P=G N + O $, where $ G $ is the gain, $ N $ is the number of photons detected, and $ O $ is the offset. If you set up the camera this way, $ G=1 $ and $ O=64 $. (To make things confusing, the units of the settings are arbitrary. (In other words, the numbers you type into the boxes are not the same as the values in the equation.)
- Set up a scene that has a large range of light intensities.
- An easy way to do this using the same apparatus you used in the previous part is to slide the 35 mm lens as far as it will go toward the camera. You should see a bright spot in the middle of the camera. Screw an iris in to the other side of the X-lookin' thing where the imaging target is mounted.
- Start with the iris about half way open. Move the iris so that it is in focus on the camera.
- Futz with the exposure, iris, and lens position until you have roughly the same number of pixels for each intensity value over the largest range you can achieve. Use the histogram plot to assess your setup. Make sure the curve goes all the way down to completely dark.
If you ever want to plot your own histogram from a saved image, here is some example MATLAB code to do just that:
[ counts, bins ] = hist( double( squeeze( exposureTest(:) ) ), 100); semilogy( bins, counts, 'LineWidth', 3 ) xlabel( 'Intensity (ADU)' ) ylabel( 'Counts' ) title( 'Image Intensity Histogram' )
Acquire movie and plot results
Once you are set up correctly, make a movie and plot the results using the procedure below:
- Capture a 100 frame movie.
- Go to the Image Acquisition window and change the Number of Frames property from 1 to 100.
- Press Acquire.
- Switch to the MATLAB console window. (Press alt-tab until the console appears.)
- Save the movie to a variable called noiseMovie by typing: noiseMovie = foo.ImageData;
- Plot pixel variance versus mean.
- Use the code below to make your plot.
noiseMovie = max( 0, double( squeeze( foo.ImageData ) ) - 64 ); pixelMean = mean( noiseMovie, 3 ); pixelVariance = var( noiseMovie, 0, 3 ); pixelMean = pixelMean(:); pixelVariance = pixelVariance(:); badOnes = pixelMean < 4; pixelMean( badOnes ) = []; pixelVariance( badOnes ) = []; [counts, binValues, binIndexes ] = histcounts( pixelMean(:), 4:4:4095 ); binnedVariances = accumarray( binIndexes(:), pixelVariance(:), [], @mean ); binnedMeans = accumarray( binIndexes(:), pixelMean(:), [], @mean ); figure loglog( pixelMean(:), pixelVariance(:), 'x' ); hold on loglog( binnedMeans, binnedVariances, 'LineWidth', 3 ) xlabel( 'Mean (ADU)' ) ylabel( 'Variance (ADU^2)') title( 'Image Noise Versus Intensity' )
Save your plot as a .png (on the plot, click on File -> Save As ->)
If you prefer to use Python, save your movie data with the save command in MATLAB and use the following code:
import numpy
import matplotlib.pyplot
import scipy.io
matlabData = scipy.io.loadmat( <PATH TO .mat FILE> )
# matlabData is a DICTIONARY containing all the variables stored in the .mat file
# make a numpy array from the noiseMovie variable in matlabData
noiseMovie = numpy.array( matlabData['staticSceneMovie'] )
pixelMean = numpy.average( noiseMovie, axis = 2 )
pixelVariance = numpy.var( noiseMovie, axis = 2 )
pixelMean = numpy.reshape( pixelMean, [ 1, -1 ] )
pixelVariance = numpy.reshape( pixelVariance, [ 1, -1 ] )
badOnes = numpy.nonzero( numpy.logical_or( numpy.less( pixelMean, 10 ), numpy.greater( pixelMean, 3900 ) ))
pixelMean = numpy.delete( pixelMean, badOnes)
pixelVariance = numpy.delete( pixelVariance, badOnes)
print( numpy.shape(pixelMean) )
binIndexes = numpy.digitize( pixelMean, numpy.arange( 10, 3900, 4 ) )
averageVariance = numpy.zeros( numpy.shape( numpy.arange( 10, 3900, 4 ) ) )
count = numpy.zeros( numpy.shape( pixelVariance ) )
for i in range( numpy.shape( pixelVariance )[0] ):
averageVariance[binIndexes[i]-1] += pixelVariance[i]
count[binIndexes[i]-1] += 1
for i in range( numpy.shape( averageVariance )[0] ):
if count[i] > 0:
averageVariance[i] = averageVariance[i] / count[i]
else:
averageVariance[i] = numpy.NAN
model = numpy.polyfit( pixelMean, pixelVariance, 1, w = numpy.divide( 1, pixelMean ) )
print( model )
#matplotlib.pyplot.ion()
matplotlib.pyplot.loglog( pixelMean, pixelVariance, marker = 'x', markerfacecolor='None', markeredgecolor='b',linestyle = 'None' )
matplotlib.pyplot.loglog( numpy.arange( 10, 3900, 4 ), averageVariance )
matplotlib.pyplot.xlabel( 'Mean (ADU)')
matplotlib.pyplot.ylabel( r'Variance ($ADU^2$)')
matplotlib.pyplot.text( 10, 3000, r'$\sigma^2_P = %0.2f \bar P + %0.2f$' % (model[0], model[1] ), horizontalalignment='left' )
matplotlib.pyplot.title( 'Pixel Variance vs Mean')
matplotlib.pyplot.show()
| |
|
When you're done, please slide the object and lenses back to where you found them at the start of the lab exercise. Make sure you have all the relevant plots and/or data saved, then clear the MATLAB workspace for the next group using the command clear all.
- Overview
- Part 1: Pre-lab questions
- Part 2: Optics bootcamp
- Part 3: Build a microscope
- Part 4: Measure stuff
Back to 20.309 Main Page