Difference between revisions of "Geometrical optics and ray tracing"

Overview

Light is an extraordinarily complicated, three dimensional, time dependent phenomenon. Completely describing a light field requires a function that quantifies the intensity, phase, wavelength, and propagation direction of light at every point in space. Needless to say, it can be difficult to conceptualize a light field. Fortunately, there is a simplified model of light called ray optics that works well in situations where the objects that interact with a light field are much larger than the wavelength of the light.

A light ray encountering an object

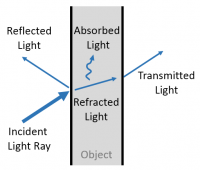
Ray optics (a.k.a. geometric optics) simplifies a light field by turning it into an abstract collection of lines that point in the direction of propagation. The lines begin at a source and go straight, until an interaction between light and matter causes a change. When a ray encounters an object, it may be:

• Reflected
• Refracted (the light is bent by the material properties of the object)
• Absorbed (often turned into thermal energy)
• Transmitted
• Scattered in a random direction
• Or some combination of the above.

The simplifications of ray optics provide a very good way to understand systems of lenses, mirrors, filters, and illumination sources. In many cases, ray optics can elucidate the function of a complicated optical system with just a few lines, triangles, and simple rules. Of course, the simplicity of ray optics comes at a cost. Ray optics glosses over important details like diffraction and interference. Because the fine details are omitted, ray optics alone does not provide insight into detailed performance characteristics like resolution.

This page introduces ray optics and discusses distortions called optical aberrations that occur in situations where one or more of the simplifying assumptions fail. Diffraction and resolution are discussed on a separate page.

The systems of optical components that we will consider in 20.309 have smooth surfaces made of non-absorbent materials. Their behavior is predominantly governed by reflection and refraction, so we won't spend a lot of time on scattering and absorption for now.

Relationship between light rays and waves

Rays point in the direction of propagation.

Representation of the field generated by a point source. The blue circles indicate peaks of the electric field at one time in a plane that includes the source. A small distance below the source, there is an interface to a medium with higher refractive index. Light propagates at a slower speed in the higher-index medium. An example ray (red line) is drawn perpendicular to the axis of propagation. The ray bends at the interface between the two media.

Relationship of manta rays to waves

Manta ray.Image by Daniel Mietchen.

Not so much. But manta rays are really cool.

Reflection and refraction

The law of reflection and Snell's law of refraction

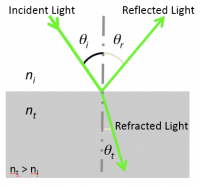
When light reflects, the angle of the reflected ray is equal to the angle of the incident ray: $ \theta_r=\theta_i $. Both angles are measured relative to a vector normal to the surface. Incident and reflected rays are in the same plane.

Light incident at an interface between media that have different indices of refraction will be partly reflected back into the first medium and partly transmitted to the second medium. Refractive index is a measure of the speed that light propagates in a medium. When the light changes speed, its direction of propagation also changes.

The transmitted light propagates at an angle

or refracted according to the Snell-Descartes law:

$ n_i\ \sin \theta_i = n_t\ \sin \theta_t $

with θ the angle measured from the normal of the boundary, $ n $ the refractive index (which has no units) of the medium, and the subscripts $ i $ and $ t $ referring to the incident and transmitted light, respectively.

• Snell's law implies that light passing from a medium of lower index to a higher index of refraction ($ n_t > n_i $) bends toward the surface normal ($ \theta_t < \theta_i $), whereas light traveling from a higher index to a lower index of refraction bends away from the normal. Remember, a higher index means a lower velocity of light in the medium.

• The index of refraction $ n $ of a transparent optical medium is defined as the ratio of the speed of light in vacuum, $ c $, by the speed of light in the medium, $ v $.

$ n = c / v $

• The index of refraction is a property of the material

Critical angle and total internal reflection

• Snell's law includes the concept of a critical angle $ \theta_c $ for the incident light ray. As the angle of the incident ray approaches $ \theta_c $, the angle $ \theta_t $ approaches 90^o. Beyond $ \theta_c $, total internal reflection takes place. In this regime the ray obeys the rules of reflection above.
• Recalling that $ \sin (90^o) = 1 $, one can derive

$ \theta_c = \sin ^{-1} \left ( {n_t \over n_i} \right ) $

• All fiber optic communication takes advantage of the phenomenon of total internal reflection. The core medium of a fiber is covered by another medium with a lower index of refraction, called the cladding. Thus if light enters the fiber at an angle less than $ \theta_c $, and if the fiber is not bent too far, then the entering light will emerge at the end of the fiber minus only losses in the fiber, plus losses due to other practicalities of the real world of course.

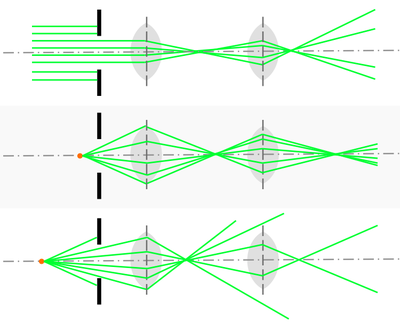
Refraction at a spherical boundary

Light being refracted at differently-shaped interfaces

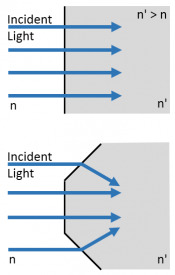
Now that we know how light refracts at a flat interface, we can understand how to manipulate the light by changing the shape of the interface. For example, if you have light coming in from the sun and want to concentrate it onto your solar cell, how can you do so with what you know about refraction?

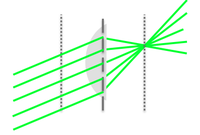
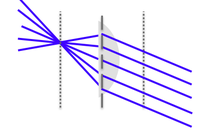
Consider the figure on the right. If we have light rays coming in perpendicular to a flat surface, based on Snell's law, the rays will pass through the second medium without changing its direction ($ \theta_i = \theta_t = 0 $). Let's pretend the gray object is a piece of glass, having a higher index of refraction than the air to its left ($ n' > n $) . If we change the angle of the interface, as in the lower panel of the figure, we can direct some of the light rays to converge, and thus be closer to our goal of concentrating light onto our solar cell. You can imagine if we made the surface spherical, we could consider Snell’s law at each small point on the interface and see that the light would eventually focus to a single spot.

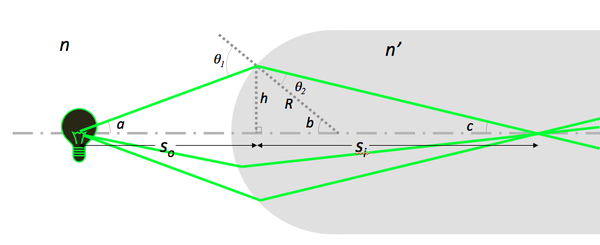
The figure below demonstrates how light rays from a point (on the light bulb) are focused to a single point by a spherical boundary between the two materials. The depicted angles and defined lengths can be used to calculate where the light will be focused.

Light rays from a point on the light bulb can converge to a point after passing through a spherical interface if certain conditions are met (explained in the following sections). Here, the index of refraction of the second medium ($ n' $) is higher than the first ($ n $). The dotted line is normal to the boundary at a specific point, with the angles corresponding to those in Snell's law. $ S_o $ is the distance from the object to the interface, $ S_i $ corresponds to the distance from the interface to the point to which the light is focused, and R is the radius of curvature

Gaussian optics assumptions

As you can see from the figure above, as we begin to deal with multiple curved interfaces, it can become complicated to solve many geometric equations to find where the light will be focused. In order to make more tractable calculations for us to use when designing our optical systems, we rely on a few first-order, or Gaussian optics, approximations:

• Paraxial (or small-angle) approximation:

Assumes that light rays make a small angle with the principle axis (a straight line perpendicular to the center of the curved surface)

$ \theta \approx \sin\ \theta \approx \tan\ \theta $

$ \cos\ \theta \approx 1 $

(These relations are obtained from the first-order terms of the polynomial expansions of $ \sin \theta = \theta - {\theta^3 \over {3!}} + {\theta^5 \over {5!}} - ... $ and $ \cos \theta = 1 - {\theta^2 \over {2!}} + {\theta^4 \over {4!}} - ... $ and are accurate to 1% if $ \theta < 10^o $.)

• Thin-lens approximation:

$ R << S_o,\ S_i $

with $ R $ defined as the radius of curvature of the lens, $ S_o $ as the distance between the lens and the object, and $ S_i $ the distance between the lens and the image.

• These paraxial and thin-lens engineering approximations simplify most optical systems by enabling the use of a short set of ray tracing rules for spherical lenses. These rules reduce many optics problems to more intuitive geometry problems.

• Deviations from these assumptions result in optical aberrations.

• More on thick lenses can be found in the book 'Optics' by Eugene Hecht (Addison-Wesley​, 2002, ISBN 0805385665).

Object and image positions

• Now, with our Gaussian optics assumptions, we can use Snell's law to predict the image position of an object, formed by a spherical surface (referring to the light bulb diagram above):

$ n\ \sin \theta_1 = n'\ \sin \theta_2 $

$ \sin \theta_1 \approx \sin a + \sin b \approx {h \over S_o} + {h \over R} $

$ \sin \theta_2 \approx \sin b - \sin c \approx {h \over R} - {h \over S_i} $

$ {n \over S_o} + {n' \over S_i} = {(n'\ - n)\over R} $

Massaging this equation gives three possible relationships between $ S_i $ and $ S_o $:

a) Light converges $ S_o > {n\ R \over (n'\ - n)}\ \Rightarrow S_i > 0 $ ,	b) Light is collimated $ S_o = {n\ R \over (n'\ - n)}\ \Rightarrow S_i \to + \infty $,	c) Light diverges $ S_o < {n\ R \over (n'\ - n)}\ \Rightarrow S_i < 0 $

Note that

• $ S_i $ does not depend on the angle $ a $.
• Light coming from a point on the filament passes through a point after refraction.
• The sign convention is that if $ S_i < 0 $, the light diverges, and a virtual image is formed at a distance $ |S_i| $ in front of the lens, on the same side of the lens as the light source (virtual images will be discussed more in a following section).

Lenses

Lens maker formula

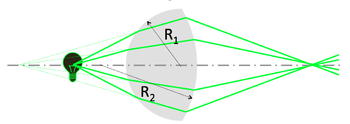
A simple lens consists of two spherical interfaces of radii of curvature $ R_1 $ and $ R_2 $. Its focal length $ f $ is given by the lens maker formula:

$ {1 \over S_o} + {1 \over S_i} = {1 \over f} = {(n'\ - n) \over n} \left ( {1 \over R_1} - {1 \over R_2} \right ) $

Bi-convex lens	Plano-concave lens

• In your ray-tracing studies, you'll use the image from the first refraction as the object for the second.
• Note the sign convention for the second surface: $ R_2 $ < 0 for a convex lens, and $ (n'\ - n) $ has opposite sign.
• Concave lens: the lens maker formula holds for $ R_1 $ < 0.

Types of spherical lenses

To minimize spherical aberrations, the general rule is to position the curved side of the lens toward the collimated/straight light.

Ray tracing

Principles

	Rule 1: Rays passing through the center of a lens are unaffected by the lens.
	Rule2 : Rays that are parallel before hitting a lens pass through the same point on the focal plane after the lens. Rule 3: Rule 1 and Rule 2 hold in reverse.

Objects and images

Imaging with a lens

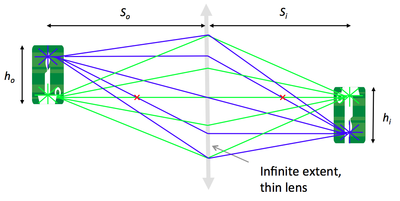
Imagine the object is made up of many point sources. After refraction, all the rays from a single point in the object plane reach the same location in the image plane. This forms a real, inverted image.

Magnification

By similar triangles, magnification is equal to the ratio of distances to the lens:

$ M = {h_i \over h_o} = {S_i \over S_o} $

A 4f microscope (construction rays shown as solid lines, additional rays as dashed lines)

You will verify this equation through the Optics Bootcamp exercise of the first problem set.

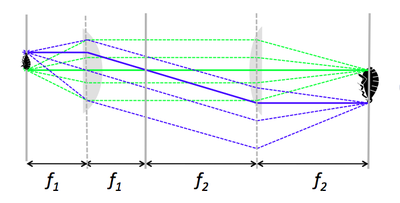
A 4 f or compound microscope

• A 4 f microscope is made of two positive lenses, placed at the sum of their focal lengths apart.
• An object (sample) placed in the focal plane of the first lens gets magnified by the ratio of focal lengths, $ f_2 / f_1 $.
• It is left as an exercise to the reader to show that the two lenses do not need to be separated by $ f_1 + f_2 $. Hint: Make clever use of Rule 3.

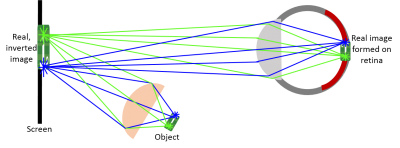
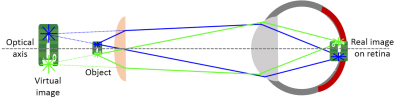
The eye as a lens

	The eye’s optical system focuses the light from each point of the object on to a point on the retina to create an image.
	When an image is projected on a screen, the projection system focuses the light from each point in the object to a corresponding point on the screen. When you view this real image, your eye focuses the light from each point on to your retina – just like it would if the object was located on the screen. (Hence, the convincing illusion.)
	You can also view a real image directly. In an optical system the image of a lens acts like the object of the next.
	You can observe a virtual image. In the virtual image, each light ray from a point on the object appears to originate from a different point in space. Unlike a real image, you cannot position a screen to show the image – there is no place that the rays come together, unless they are refracted by another lens (your eye, in this case). The image in a magnifying glass is virtual.

Aperture and field stops

Aperture stop and image brightness

• The aperture stop of an imaging system is the optical element that limits angle of rays passing through the system from a source on the optical axis.
• For an off-axis object, the chief ray is the ray that passes through the center of the aperture stop, and the marginal rays are those that pass through the edge of the aperture stop.
• The size of the aperture stop determines the light-gathering capability of an instrument, and thus the brightness (or irradiance in W/m²) of its images.
• Typically in a microscope, as opposed to a photographic camera, the aperture stop will be the objective lens rather than an aperture before the lens as shown here.

The aperture stop in system can be (top) the left diaphragm, (middle) the first, left lens, or (bottom) the second, right lens.

Light-gathering power of oil-immersion and air-immersion lens, showing that $ \alpha_{oil} > \alpha_{air} $.

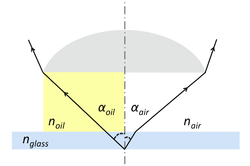
Numerical aperture

• The numerical aperture (NA) is another important measure that characterizes the light-gathering power of a lens.

$ NA = n\ \sin \alpha $

where $ n $ is the index of refraction of the medium between the object (sample) and the lens and $ \alpha $ is the half-angle defined by the limiting ray. The limiting ray is is the last ray not blocked by any aperture.

• An oil-immersion objective lens will thus have a greater NA than an air-immersion objective lens ($ n_{oil} > n_{air} $ and $ \alpha_{oil} > \alpha_{air} $; indeed, little refraction occurs at the glass-oil interface where $ n_{oil} \approx n_{glass} $). Notice the much smaller angle of the limiting ray (drawn, but not labeled, near the point of origin in the diagram) in the case of air-immersion lens.

Field stop and field of view

• The field stop is the optical element that blocks off-axis rays passing through the center of the aperture stop (i.e. the chief rays).
• The field stop determines how much of the object can be viewed, in other words: the field of view of the imaging system.
• In your 20.309 microscope, the field stop will be the CCD camera.
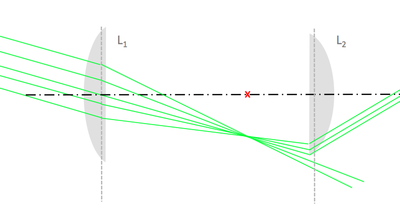
• A finite-size lens can also act as a field stop. Below is an illustration of this vignetting effect: a cone of light rays from an off-axis object is not transmitted in its entirety, but rather partially cut off by the field stop of the system, L₂'s rim.

Further reading

• Optical aberrations
• Physical optics and resolution

References