Difference between revisions of "Geometrical optics and ray tracing"
From Course Wiki
MAXINE JONAS (Talk | contribs) |
MAXINE JONAS (Talk | contribs) |
||
| Line 38: | Line 38: | ||
|c) <math> S_o = {n\ R \over (n'\ - n)}\ \Rightarrow S_i < 0</math> | |c) <math> S_o = {n\ R \over (n'\ - n)}\ \Rightarrow S_i < 0</math> | ||
|} | |} | ||
| + | |||
| + | |||
| + | ==Lenses== | ||
| + | |||
| + | ===Lens maker formula=== | ||
| + | |||
| + | A simple lens consists of two spherical interfaces. Its focal length <math>f</math> is given by the lens maker formula: | ||
| + | :<math> {1 \over S_o} + {1 \over S_i} = {1 \over f} = {(n'\ - n) \over n} \left ( {1 \over R_1} - {1 \over R_2} \right )</math> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | !width="350"| Convex lens | ||
| + | !width="350"| Plano-concave lens | ||
| + | |- | ||
| + | |[[Image: 20.309 130819 LensMaker2.png|frameless|center|350px]] | ||
| + | |[[Image: 20.309 130819 ConcaveLens.png|frameless|center|200px]] | ||
| + | |} | ||
| + | |||
| + | * Use the image from the first refraction as the object for the second. | ||
| + | * Note the sign convention for the second surface: <math>R_2</math> < 0 for a convex lens, and <math>(n'\ - n)</math> has opposite sign. | ||
| + | * Concave lens: the lens maker formula holds for <math>R_1</math> < 0. | ||
| + | |||
| + | |||
{{Template:20.309 bottom}} | {{Template:20.309 bottom}} | ||
Revision as of 17:25, 19 August 2013
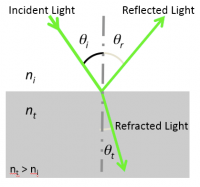
Refraction and reflection
Refraction and reflection at a boundary
- The Snell-Descartes law or law of refraction stipulates that
- $ n_i\ \sin \theta_i = n_t\ \sin \theta_t $
- with θ the angle measured from the normal of the boundary, $ n $ the refractive index (which is unitless) of the medium, the subscripts $ i $ and $ t $ referring to the incident and transmitted light, respectively.
- The law of reflection states that θi = θr
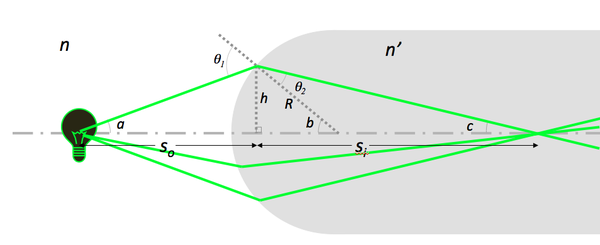
Refraction and reflection at a spherical interface
With the assumptions:
- Paraxial approximation: θ ≈ sin θ ≈ tan θ
- Thin lens approximation: $ R << S_o,\ S_i $
Snell's law predicts that
- $ n\ \sin \theta_1 = n'\ \sin \theta_2 $
- $ \sin \theta_1 \approx \sin a + \sin b \approx {h \over S_o} + {h \over R} $
- $ \sin \theta_2 \approx \sin b - \sin c \approx {h \over R} - {h \over S_i} $
- $ {n \over S_o} + {n' \over S_i} = {(n'\ - n)\over R} $
Note that
- Si does not depend on the angle $ a $.
- Light coming from a point on the filament passes through a point after refraction.
- We shall revisit these assumptions later.
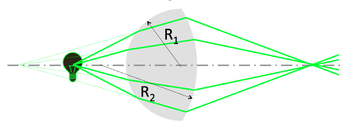
| a) $ S_o > {n\ R \over (n'\ - n)}\ \Rightarrow S_i > 0 $ , | b) $ S_o = {n\ R \over (n'\ - n)}\ \Rightarrow S_i \to + \infty $, | c) $ S_o = {n\ R \over (n'\ - n)}\ \Rightarrow S_i < 0 $ |
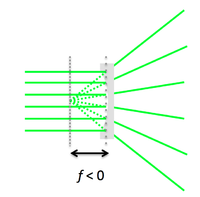
Lenses
Lens maker formula
A simple lens consists of two spherical interfaces. Its focal length $ f $ is given by the lens maker formula:
- $ {1 \over S_o} + {1 \over S_i} = {1 \over f} = {(n'\ - n) \over n} \left ( {1 \over R_1} - {1 \over R_2} \right ) $
| Convex lens | Plano-concave lens |
|---|---|
- Use the image from the first refraction as the object for the second.
- Note the sign convention for the second surface: $ R_2 $ < 0 for a convex lens, and $ (n'\ - n) $ has opposite sign.
- Concave lens: the lens maker formula holds for $ R_1 $ < 0.