Bode plots and frequency response

Overview

Only two things can happen to a sine wave passing through a linear, time-invariant system: it's magnitude can be changed; and the signal can be delayed. The delay and percentage change in the magnitude are a function of frequency. A transfer function, H(f), is a complex-valued function of frequency that specifies the magnitude and phase shift of a particular system for all frequencies. The change in amplitude is often called the gain, and the delay is usually thought of in terms of a phase shift of the sine wave.

One way to visualize a transfer function is to make two plots. The first plot shows the gain verses frequency on a set of log-log axes. The second plot shows the phase shift versus log frequency.

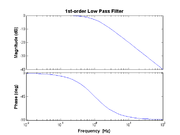
A Bode plot is a log-log representation plot of the magnitude of a transfer function versus frequency. In a Bode plot, only straight line segments are used to approximate the transfer function. At a critical or cutoff frequency, there is an abrupt change in slope in the transfer function instead of a smooth transition (e.g., from pass band to stop band).

First-order R-C low-pass filter.

For example, consider a simple RC low-pass filter with the transfer function is given by

$ H(f) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j2\pi f RC} $

In this case the cutoff frequency is given by $ f_C = 1/(2\pi RC) $. In the Bode plot of this function, a straight line segment with zero slope for $ f < f_C $ represents the pass band of the filter while a line with a slope of −1 for $ f > f_C $ represents the stop band.

Bode plot of low-pass transfer function.

More examples

High-pass

$ H(f) = \frac{j2\pi f \tau_{\rm HP}}{1 + j2\pi f \tau_{\rm HP}} $

$ H(f) = \frac{j f / f_{\rm HP}}{1 + j f / f_{\rm HP}} $

Second-order low-pass

$ H(f) = \left(\frac{1}{1 + j2\pi f \tau_{\rm LP}}\right)^2 $

$ H(f) = \left(\frac{1}{1 + j f / f_{\rm LP}}\right)^2 $

Band pass

$ H(f) = \frac{j2\pi f \tau_{\rm HP}}{1 + j2\pi f \tau_{\rm HP}} \times \frac{1}{1 + j2\pi f \tau_{\rm LP}} $

$ H(f) = \frac{j f / f_{\rm HP}}{1 + j f / f_{\rm HP}} \times \frac{1}{1 + j f / f_{\rm LP}} $