Complex Number Review
From Course Wiki
Overview
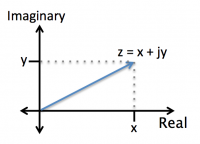
Complex numbers include a real component and an imaginary component, which involves the imaginary number $ j = \sqrt{-1} $. We can represent a complex number like this: $ z = x + jy $, where $ x $ is the real part and $ y $ is the imaginary part. Complex numbers can be represented on a plot as shown on the right, where the horizontal axis corresponds to the real part and the vertical axis corresponds to the imaginary part.When complex numbers are added together, the real components add to real components, and the imaginary components add to imaginary components. Similarly, when complex numbers are subtracted, the real parts are subtracted from each other, and the imaginary parts are subtracted from each other.
Since we are often dealing with sinusoidal waveforms, it can be helpful to think of complex numbers in exponential form. According to Euler's identities,
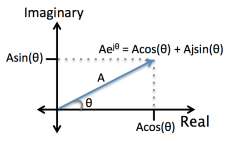
- $ e^{j \theta} = cos(\theta) + j sin(\theta) $
- $ cos(\theta) = {e^{j\theta} + e^{-j\theta}\over 2} $
- $ sin(\theta) = {e^{j\theta} - e^{-j\theta}\over 2} $
Finding the magnitude
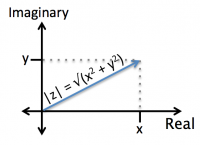
- In the rectangular form of the complex number $ z = x + jy $, we can see that the magnitude of $ z $ (the length of the blue arrow in the plot below) is:
- $ |z| = \sqrt{x^2 + y^2} $
- In exponential form, we can see that the magnitude of $ Ae^{j \theta} $ is:
- $ |Ae^{j \theta}| = A $
- Thus, when two complex numbers are multiplied, their magnitudes multiply.
- Similarly, when two complex numbers are divided (as we often see in transfer functions), their magnitudes are divided.
- For example, $ |{Ae^{j \theta} \over Be^{j \theta}}| = {A \over B} $
- Transfer function example: If you have a transfer function that looks like $ H(\omega ) = {1 \over 1+ j \omega RC} $, the magnitude of this function is given by the magnitude of the numerator ($ 1 $) divided by the magnitude of the denominator ($ \sqrt {1^2 + (\omega R C)^2} $):
- $ |H(\omega )| = {1 \over \sqrt {1 + \omega ^2 R^2 C^2}} $
Finding the phase
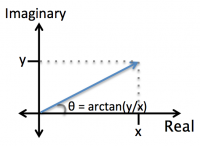
- To the find the phase of a complex number $ \ang z $, where $ z = x + jy $, we find the value for $ \theta $ as demarcated in the plot below.
- $ \ang z = \theta = arctan({y \over x}) $
- This means that a real number, having no imaginary component, has a phase of 0°.
- Meanwhile, a purely imaginary number has a phase of 90°.
- When multiplying or dividing complex numbers, one can more clearly see what happens to the phase when using exponential form. As you know,
- When multiplying exponentials, the exponents add
- When dividing exponentials, the exponents subtract.
- For example, $ {Ae^{j \theta_1} \over Be^{j \theta_2}}= {A \over B} e^{j(\theta_1 - \theta_2)} $.
- Transfer function example: If you have a transfer function that looks like $ H(\omega ) = {1 \over 1+ j \omega RC} $, the phase of this function is given by the phase of the numerator ($ 0 $) minus the phase of the denominator ($ arctan(\omega R C) $):
- $ \ang H(\omega ) = -arctan(\omega R C) $