20.109(F21):M1D6
Contents
Introduction
In this module we used two methods to assess DNA damage and repair in response to treatment with H2O2 +/- As: the γH2AX assay and the CometChip assay.
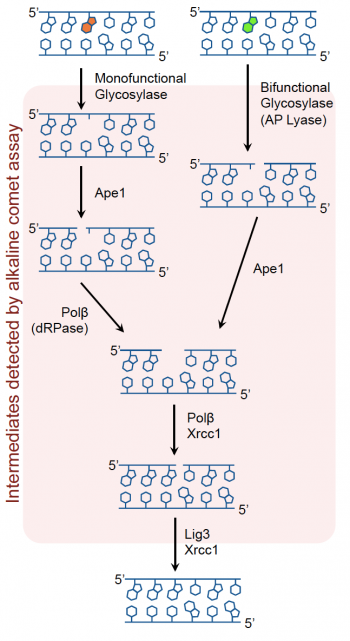
Recall that oxidative damage results in DNA lesions that are repaired via the BER pathway (see image to the right). The BER pathway is critical in the removal of small, non-helix distorting lesions from DNA. If not repaired, these lesions can result in potentially detrimental mutations.The core BER pathway includes only four proteins that function to remove the damaged base and replace it with the correct base. First, a DNA glycosylase recognizes that a damaged base is present in the DNA and cleaves an N-glycosidic bond, which creates an apurinic or apyrimidinic site (referred to as an AP site in both cases). Different DNA glycosylases recognize different types of base lesions. Second, the DNA backbone is cleaved to create a single-strand DNA nick by either a DNA AP endonuclease or a DNA AP lyase. Next, a DNA polymerase incorporates the correct base using the sister strand as a template. Last, a DNA ligase completes the repair by sealing the single-strand nick, which restores integrity to the helix. It is important to recognize that the oxidative damage caused by H2O2 does not generate DNA strand breaks, instead the BER pathways generates single-strand breaks as part of the repair process! Exposure to As potentially exacerbates this by inhibiting the ligation step that is crucial in the final step of the BER pathway.
So how does the biology fit into the experiments used to assess DNA damage and repair in response to treatment with H2O2 +/- As?
In the γH2AX assay, DNA double-strand breaks are visualized using immunofluoresence microscopy. When a DNA double-strand break is introduced into the DNA, the H2AX histones near the break are phosphorylated. Upon phosphorylation H2AX is referred to as gamma-H2AX. Given that only H2AX histones near the site of DNA damage are phosphorylated, γH2AX is a useful target when determining the abundance and location of double-strand breaks. Remember that the DNA damage expected to occur in response to H2O2 is single-stranded breaks. The logic for performing the γH2AX experiment is that multiple single-stranded breaks that are not repaired will lead to double-stranded breaks.
Today you will analyze data acquired using the CometChip assay. The CometChip is a method that allows for the direct measurement of single-strand breaks. In this assay cells are treated, loaded into the CometChip, then lysed to release the DNA into the microwell. Following cell lysis, the CometChip is incubated in an alkaline buffer that unwinds the DNA. This step allows for all types of DNA damage to be detected. Lastly, gel electrophoresis is used to separate the DNA fragments. DNA fragments migrate away from the microwell and generate a comet tail that is a measure of the extent of DNA damage.
One final aspect of our experiments that is important to interpreting the results is that we measured DNA damage over time so that repair could be assessed. The level of DNA damage was measured over a timecourse in both assays that were used. By determining the amount of DNA damage that persisted over time after the H2O2 +/- As treatment, it is possible to make inferences regarding the extent of repair that occurred in the treated cells.
Protocols
Part 1: Participate in Communication Lab workshop
Our communication instructor, Dr. Prerna Bhargava, will join us today for a discussion on writing paper titles and abstracts.
Part 2: Image CometChip experiment
To ensure you are familiar with the steps involved in imaging the CometChip experiment, please watch the video tutorial linked here: [CometChip Imaging].
Part 3: Analyze CometChip images
To complete this analysis, you may chose to use a lab computer (one per group) or your personal computer.
First, obtain the CometChip images from the Dropbox folder titled 'CometChip files'. Copy the image files (there should be 39 total) to a folder on your computer for the analysis!
If you use your personal computer, you will also need to download the Matlab code from the 'Matlab Code' folder. You may chose to run Matlab on your computer, or by using the online Matlab server found here: Matlab Online. Please note that you will need to make an account with Matlab using your MIT email address and use the MIT software license for free access. Instructions below are for Matlab online.
Stack images using ImageJ
- The script you will run will combine images from the same well into a stacked image and rename the files for the subsequent Matlab script to recognize them.
- Open ImageJ from Applications.
- Go to Plugins → Macros → Run...
- Select script "GenImageStacks_singleimage.txt" within the Documents\MATLAB\CometChip Analysis directory
- Choose the appropriate source directory that contains your image files.
- This will be the folder into which you copied the image files on your computer.
- Create a destination directory by selecting New Folder and naming the folder appropriately (eg. "180927M059_H2O2_stacked").
- Click Choose.
- ImageJ will create the stacked images in ~2 min.
- Please do not hit any additional keys until this process is completed.
- Confirm that the stacks are in the destination directory.
- Open the directory you just created, containing your stacked images.
- You should see one .tif image stack per well.
- Close ImageJ.
Optimize analysis parameters using MATLAB
- Open MATLAB online. You will need to allow popups in your browser for the analysis.
- On the menu bar chose '+ New → Folder' and title that folder "CometChip Analysis".
- Upload the contents of the 'Matlab Code' folder from Dropbox to this folder. Note: you cannot upload folders from your computer into this interface, so each file must be uploaded individually, including files from the poi library.
- Create a folder titled "Stacked Images" and upload the images you produced in ImageJ.
- Be sure that "CometChip Analysis" is the current folder.
- Run the guicometanalyzer.m file by double clicking on the file in the folder and selecting "Run" from the menu, or by selecting "run" on the right-click menu.
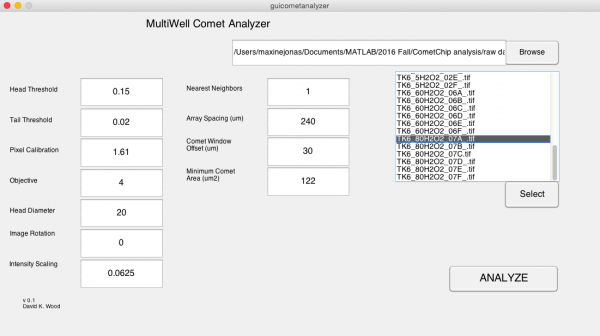
- In the MultiWell Comet Analyzer window:
- Check that the Pixel Calibration value is 1.61.
- Check that the Image Rotation value is 0 if your tails are to the right. Image Rotation should be 180 if your tails are going to the left.
- Check that the Array Spacing (μm) is 240.
- Check that the Head Diameter value is 20.
- Confirm the settings with the image below.
- Click Browse.
- Select the stacked image directory you created in Matlab.
- Click Open.
- From the image stack files loaded to the MultiWell Comet Analyzer window, choose ONE image that is expected to show DNA damage. You are just using this image to optimize the analysis parameters.
- The chosen file should be highlighted.
- Click Select.
- Click Analyze.
- Click "Yes" when the dialog box appears and asks if you want to run the program in "debug mode."
- Please do not hit any additional keys until this process is completed.
- In the MATLAB command window you will see the number of comets to be analyzed. The same number of figures should be generated.
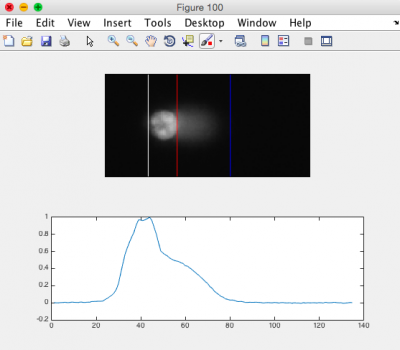
- Review the generated images.
- Ensure that the head of the comet is bracketed by a white line on the left, and a red line on the right. The tail should be bracketed by the red line and a blue line on the right. See the image to the right for an example.
- You may need to adjust the "Tail Threshold" value so that the tail is identified appropriately and/or the "Head Threshold" value so that the head is identified appropriately.
- Note: it is okay if some of the images do not appear correct according to the above criteria; however, the majority of your images should be correct.
- In the Command Window type "close all."
- If you need to adjust your parameters, repeat this process again until you find the optimal parameters for your analysis.
- Find the guicometanalzyer window.
- Adjust parameters as needed and repeat steps above by continuing to run in "debug mode."
- Type "close all" when done, but leave Matlab open.
Measure head and tail lengths using MATLAB
- Find the guicometanalyzer window
- If it has disappeared, run the script again by typing "guicometanalyzer" in the command window.
- In the MultiWell Comet Analyzer window, confirm the parameters as above.
- Click Browse.
- Select the stacked image directory you created with ImageJ.
- Click Open.
- Highlight all stack files in the MultiWell Comet Analyzer window.
- Click Select.
- Click Analyze.
- Click "No" when the dialog box appears and asks if you want to run the program in "debug mode."
- Confirm that there is a .txt file for each stack in your folder.
- Each macrowell that was imaged has one .txt file. The .txt file for each macrowell contains the data for the individual comet tails that were measured from each microwell.
- The .txt files will save in the same folder that contains the .tif image files.
In your laboratory notebook, complete the following:
- Review the data in the .txt files for two macrowells per treatment condition (no H2O2, 0 min, 15 min, 30 min, and 60 min).
- Are the values consistent across % tail DNA measured for the individual comets?
- Do you have confidence in these data? Why or why not?
Analyze CometChip data
The data from the CometChip experiment were compiled into an Excel spreadsheet (linked here). Use this spreadsheet to analyze the data for each of the treatments tested.
- First, orient yourself to the data that are provided in the spreadsheet.
- The values grouped together in the table are for the samples that were treated with 20 μM H2O2. The values at the bottom of the sheet are for the no H2O2 samples.
- The information for the timepoints (0 min, 15 min, 30 min, and 60 min) is across the top. Each condition was tested in triplicate so wells A1, A2, and A3 are replicates.
- The information for the As concentration exposure (0 μM, 2 μM, and 10 μM) is down the left side.
- Average the replicate samples for each condition and plot the data using a line graph.
- To represent the data as a timecourse, use t = -15m for the no H2O2 value. For the remaining data, use t = 0, t = 15, t = 30, and t = 60 to indicate the length of time that repair was allowed to occur following H2O2 treatment. Time should be represented on the x-axis.
- On the y-axis, plot the averaged % Tail DNA value for each condition.
In your laboratory notebook, complete the following:
- Attach the spreadsheet that contains your analyzed CometChip data.
- Compare the analyzed data to the raw images that were acquired for each of the treatment conditions.
- Review 2-3 of the .tif files for each condition tested (these are the image files that you copied into a folder on your computer).
- Do the images appear consistent with the values in the analyzed data?
- Do you have confidence in these data? Why or why not?
- Select 1-2 comets for each condition to serve as representative images in your Data summary. Representative images are often included in figures with the analyzed data to show the reader the raw form of the data. It also provides context for how the experiment was performed.
Next day: Analyze data using statistical methods