Spring 2011:Optical Trapping Lab
Contents
Team FTS
Huayu & Cory
XY position detector calibration
Roll Off
Stoke
Equipartition
for 10 mW : 2.09*10^-9 N/m
Team Humble
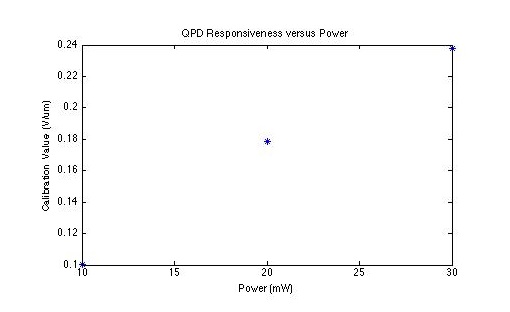
XY position detector calibration
Trap stiffness by equipartition theorem
These values are off by about 8 orders of magnitude. This graph is up temporarily until I figure out what is going wrong with my calculations.
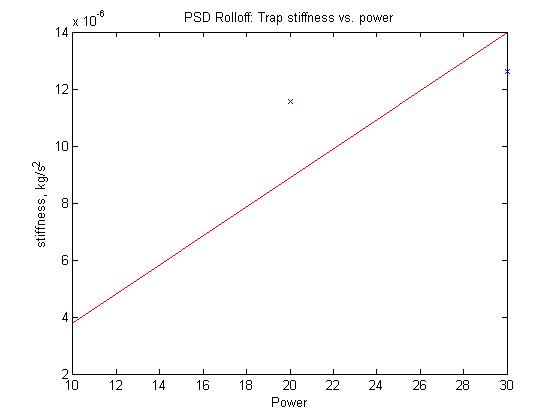
Trap stiffness by PSD rolloff
These values are about 2 orders of magnitude larger than those found in the OTKB document.
Alternative Attempt for Team Humble
(by Emily)
Not only is this last method trending the wrong way, but it is many orders of magnitude off from the previous two. This could be due to errors in the data collection or (and more likely) errors in data manipulation calculations.
Trap stiffness by Stokes' theorem
These values are about the correct order of magnitude, but the slope of the graph should be positive, not negative! Again, this graph is up temporarily until I can figure out what data processing mistakes are going on.
Attempt #3 for Team Humble
by Kristin
The goal of this lab was to measure the effective spring constant ("trap stiffness") of the optical trap system.
3 samples were taken: 10mW, 20mW, and 30mW. All graphs shown are for the 10mW sample. Similar manipulation was done for the 20 and 30 mW samples, and those results are shown at the end.
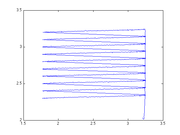
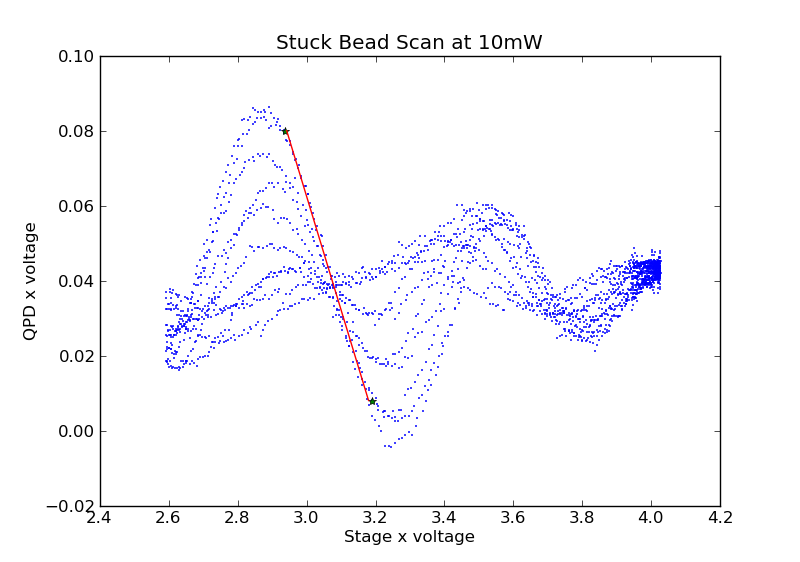
XY Scan:
From this we learned that the the optical trap scanned past the center of the bead at t = 861 time units. It is the time when the bead moved the least along the X axis (red) for the most amount of drive on the Y axis (blue). That is, if we are oscillating in the exact center of the bead, then dragging the bead up-and-down should not move it left-and-right very much.
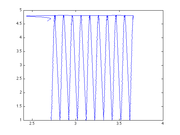
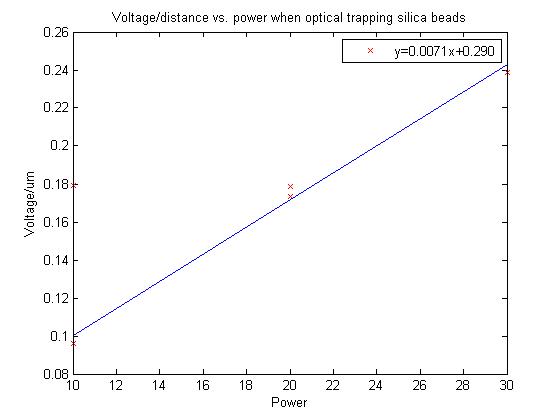
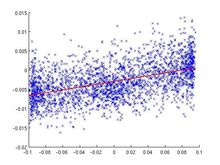
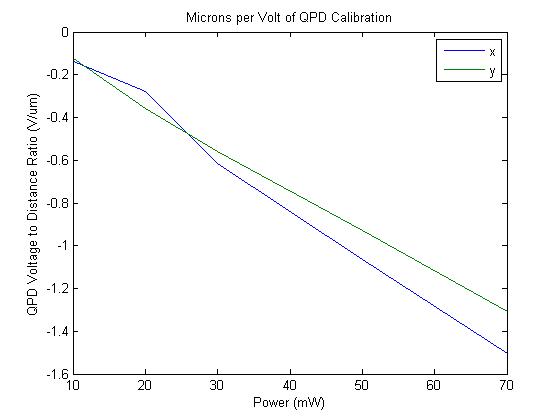
Determine calibration constant:
Here we learn the conversion between volts and distance for our particular system. The slope of this line = QPD volts / stage movement volts. The stage has been determined to move 2.22e-6 meter/volt. so slope/2.22 = QPD volt/um.
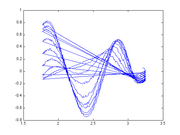
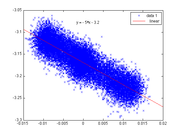
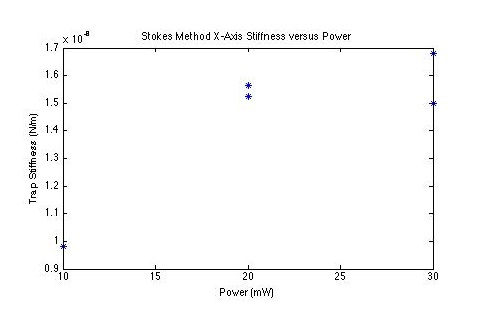
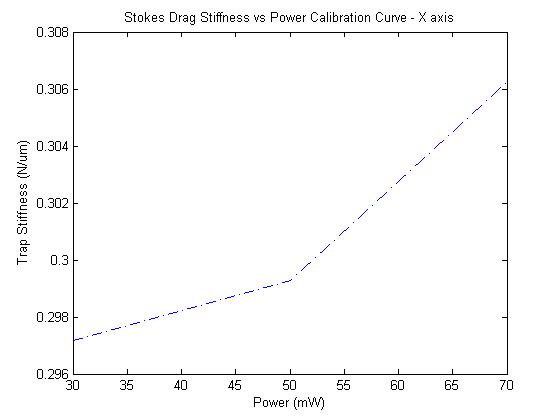
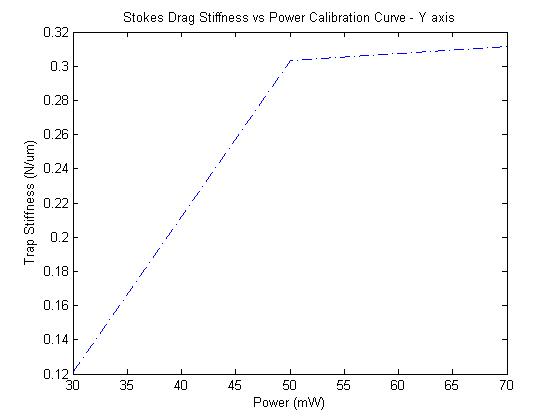
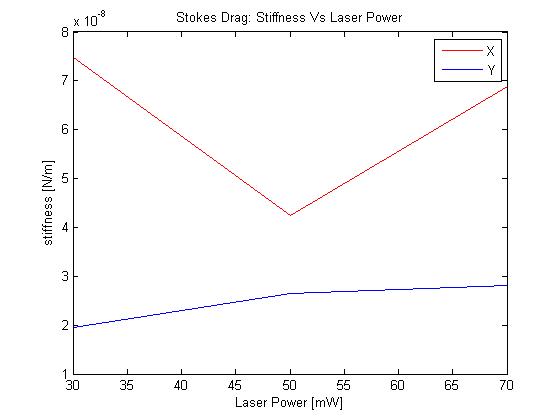
Stokes-Drag:
So one of the major forces that the optical trap must overcome to move the bead, is the drag force from the surrounding fluid. According to Stokes' law, F = 6πrv*visoscity = kx. A line was fit to this to estimate k: .3148e-3. The magnitude was kept positive to maintain a consistent sign convention.
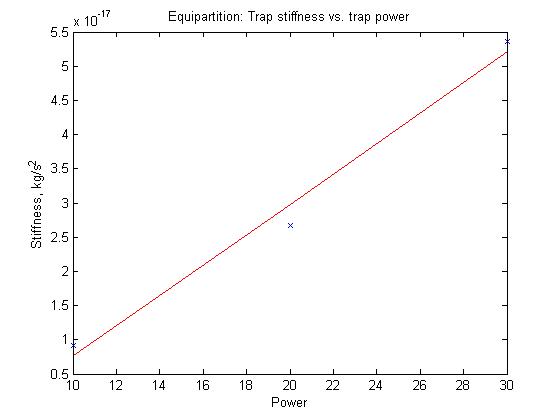
Equipartition Theorem:
According to the equipartition theorem,
(3/2)kBT = thermal energy
When holding a bead in place, it is these thermal motions that the optical trap must counteract. Thus,
(1/2)kx2 = potential energy from OT "spring" = (3/2)kBT
We solve for k, and find that k = 2.315e-07.
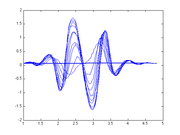
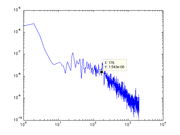
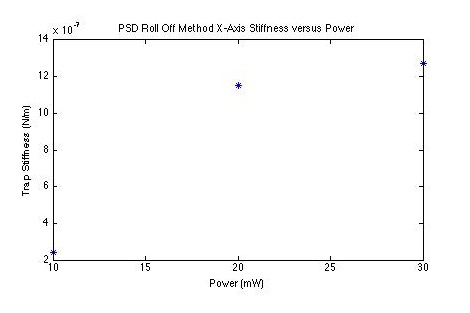
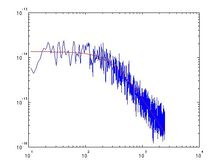
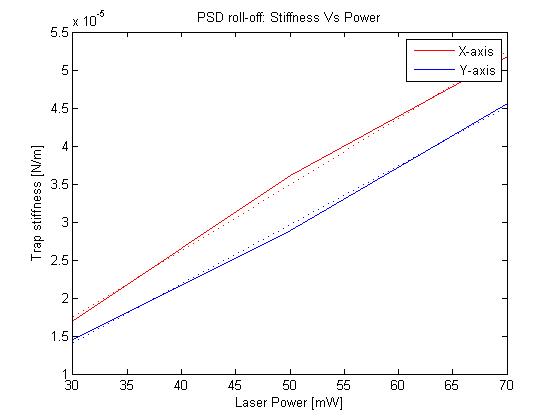
PSD roll-off:
The final method for estimating the spring constant uses the power spectral density of the bead's thermal motion. It turns out that the corner frequency (fo) of the power spectrum is related to the trap stiffness:
k = 2πfoβ
where β = 3πηd, d = bead diameter, η = viscosity of medium.
We find fo by fitting the form of the power spectrum to the actual power spectrum:
fo can be extracted from the form.
We do so, and find that k = 1.834e-05.
Results:
| 10mW | 20mW | 30mW | |
|---|---|---|---|
| Stokes-Drag | 3.148e-04 | 4.508e-04 | 3.550e-04 |
| Equipartition | 2.315e-07 | 5.1e-09 | 2.141e-07 |
| PSD roll-off | 1.834e-05 | 1.613e-05 | 2.907e-05 |
Discussion:
Alas, the results do not look great. Not only are the different methods orders of magnitude away from each other, but also the 10mW, 20mW, and 30mW do not increase proportionally as expected. One explanation is that the bead may not have been completely attached to the coverslip. This would have contributed additional forces and made the Stokes-Drag estimation too large, and indeed the S-D coefficient is much larger than the other two. The equipartition method, likewise, is vulnerable to other factors that may influence a trapped bead's motions, such as a slight flow in the medium. Failure to include these methods would make this method's trap stiffness too small - and indeed, the kequipartition is the smallest of the three. The PSD roll-off method is the most accurate, because it does not make assumptions about what is causing the bead's motions - it merely records them and extracts information from them. However, it is still an approximation, and still susceptible to poor fitting or other errors. Despite this, it is still the best estimate of the trap stiffness.
Team Watson (Drago)
XY position detector calibration
Although the Y axis plot looks OK, I'm not sure of what happened to the X axis one
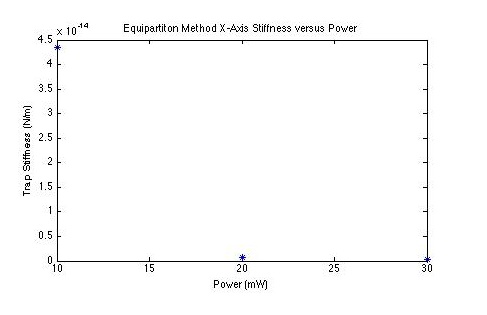
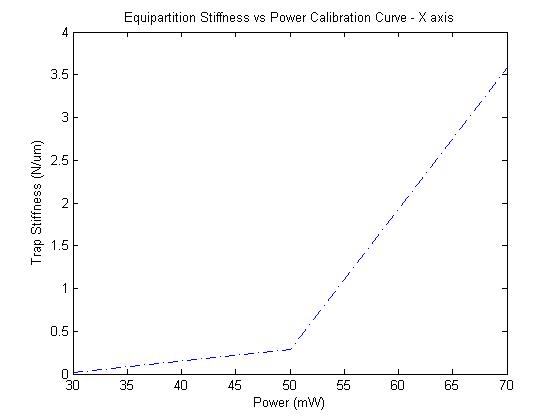
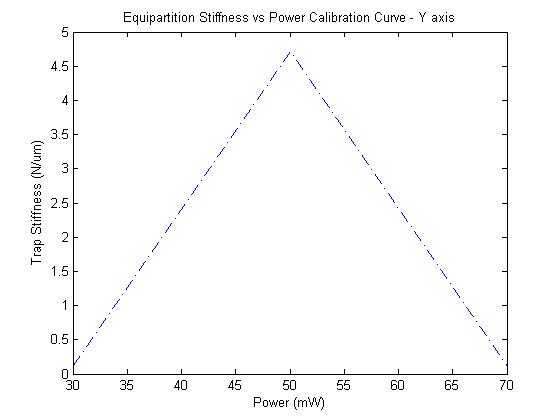
Trap stiffness by equipartition theorem
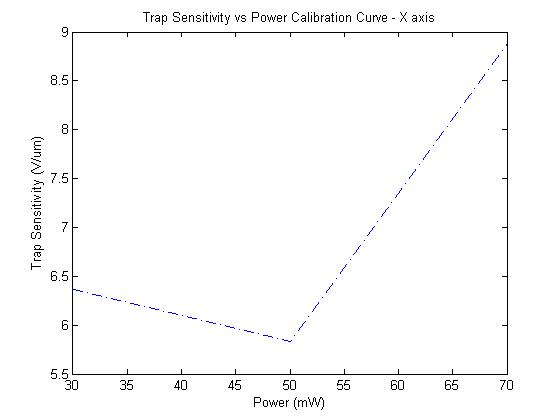
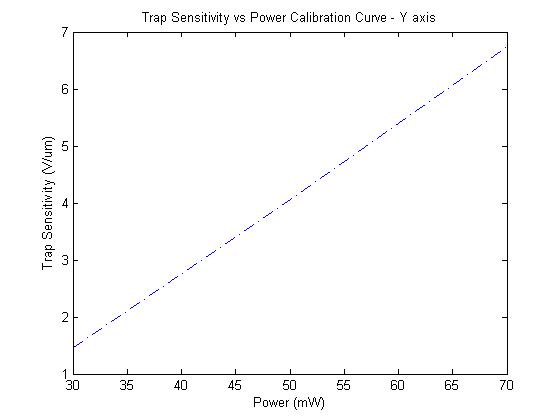
The X-axis plot follows the expected trend of higher stiffness with higher power, but the Y axis has a very off-line measurement, although the orders of magnitude seem right.
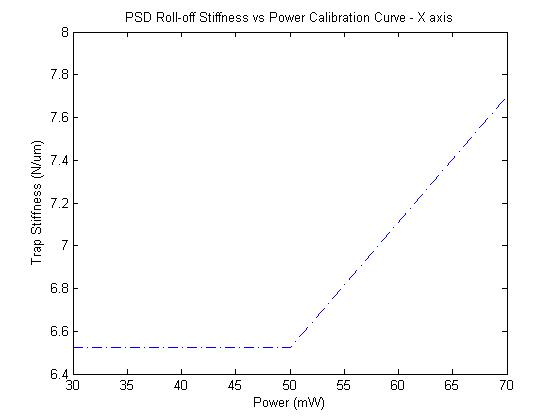
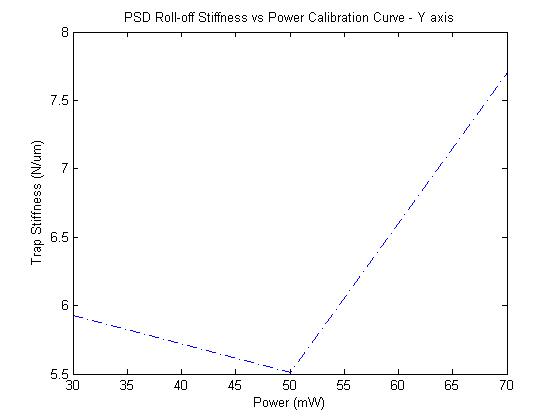
Trap stiffness by PSD rolloff
Both of these plots are right around the expected value, although they are around twice the values found for the Equipartition method (maybe there are some conversion errors).
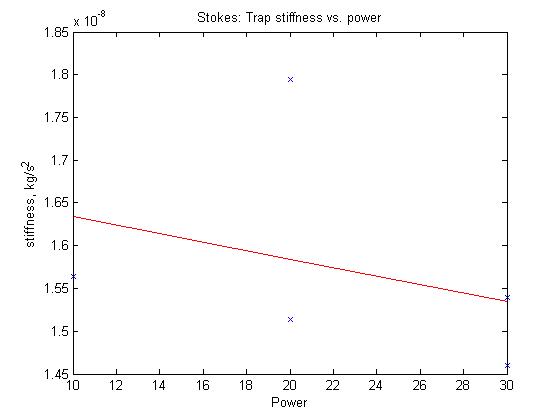
Trap stiffness by Stokes' theorem
Finally, this method seems to follow the expected trend, but its values are around an order of magnitude off from the previous methods. Again, this may be due to unit conversion issues (currently revising).
Team Watson (Emmanuel)
XY position detector calibration
- QPD_XY[V/um] = 3.38e-4 * Power[mW] + 1.6e-3
- QPD_YX[V/um] = 4.60e-4 * Power[mW] + 8.5e-3
Trap stiffness by equipartition theorem
- Equipart_stiff for X axis: kg/s^2 = 4.57e-16 * Power[mW] + 5.14e-16
- Equipart_stiff for Y axis: kg/s^2 = 3.37e-16 * Power[mW] + 3.85e-16
Trap stiffness by PSD rolloff
- PSD roll-off stiff for X axis: kg/s^2 = 1.8e-15 * Power[mW] - 51.6e-15
- PSD roll-off stiff for Y axis: kg/s^2 = 1.9e-15 * Power[mW] - 60.6e-15
Trap stiffness by Stokes' theorem
Team with Brian, Siv, Gustavo
The following anaOpticalTrapCalibBross.jpglysis is done with data collected by "Team Watson" unless noted otherwise.
Power Spectral Density roll-off
Here, we use the free bead, fixed stage data from "Team GustavSiv".
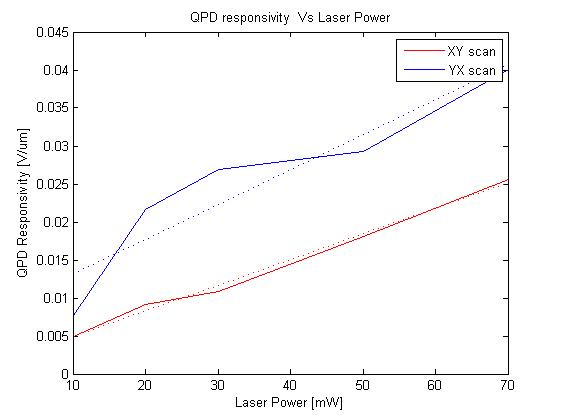
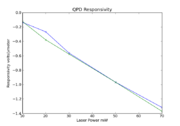
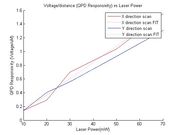
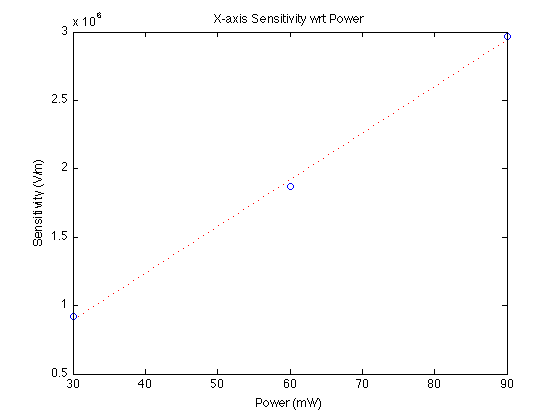
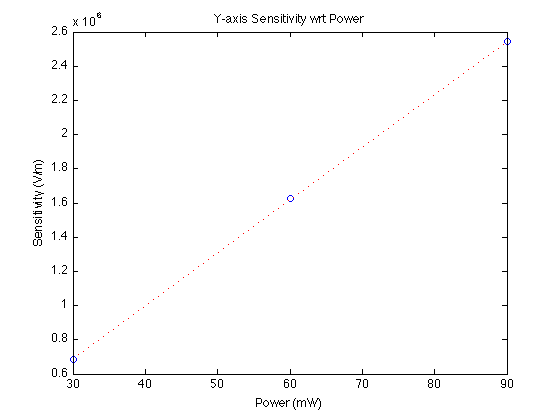
QPD Responsivity
To perform the next methods, it is necessary to calibrate the QPD.
The procedure depicted in the above graphs is repeated for each measurement, in each of the x and y axes.
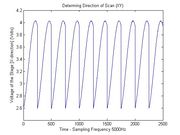
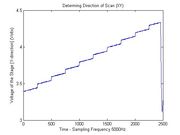
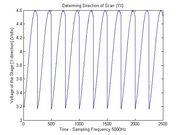
===QPD Responsivity=== (another analysis) This analysis is using the same data to generate the QPD responsivity again. Determining Direction of Scan (XY) - X direction
Determining Direction of Scan (XY) - Y direction
Determining Direction of Scan (YX) - X direction
Determining Direction of Scan (YX) - Y direction
QPD Responsivity vs Laser Power
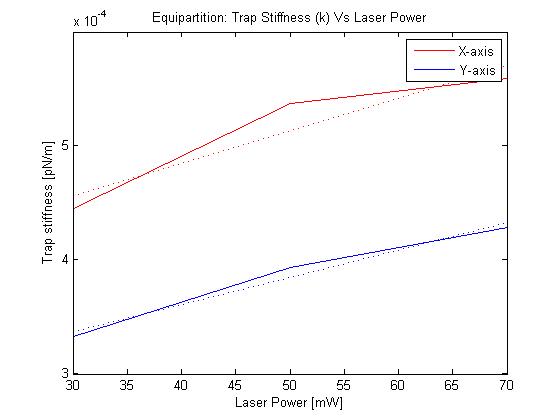
Equipartition Method
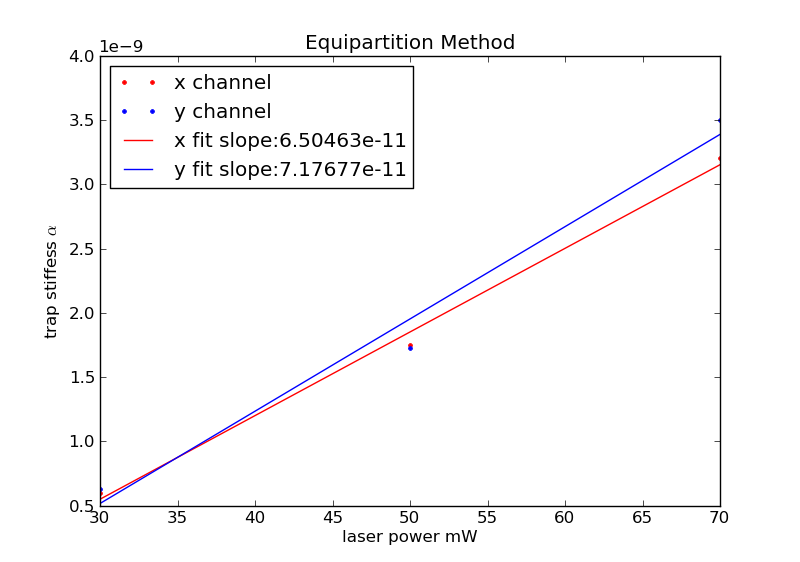 The equipartion method gives results which are off by several orders of magnitude from the expected trap stiffness.
The equipartion method gives results which are off by several orders of magnitude from the expected trap stiffness.
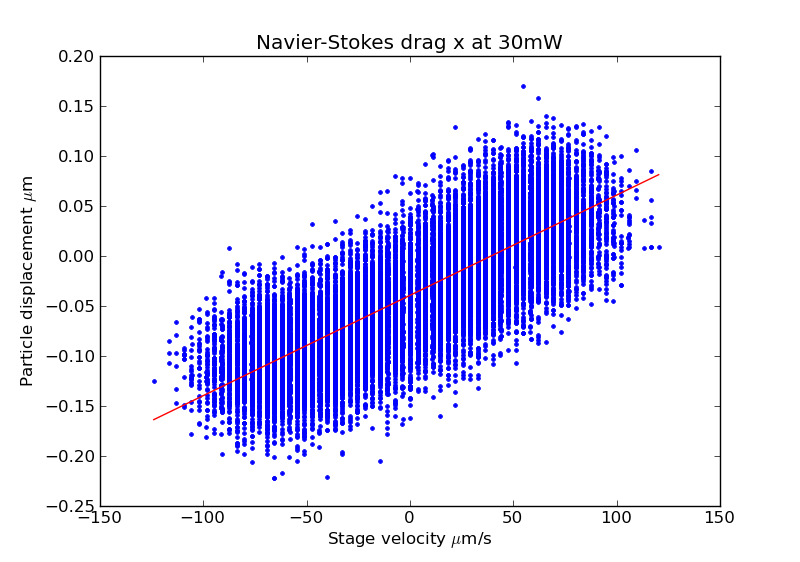
Better news here. The stage is swept back and forth and the amount of displacement of a free (as in not adhered to the cover slip, but trapped by the laser) bead is plotted over stage velocity.
The best fit line to the data gives a measure of trap stiffness. If the trap were very stiff, then the particle would move very little while the fluid moves around it.
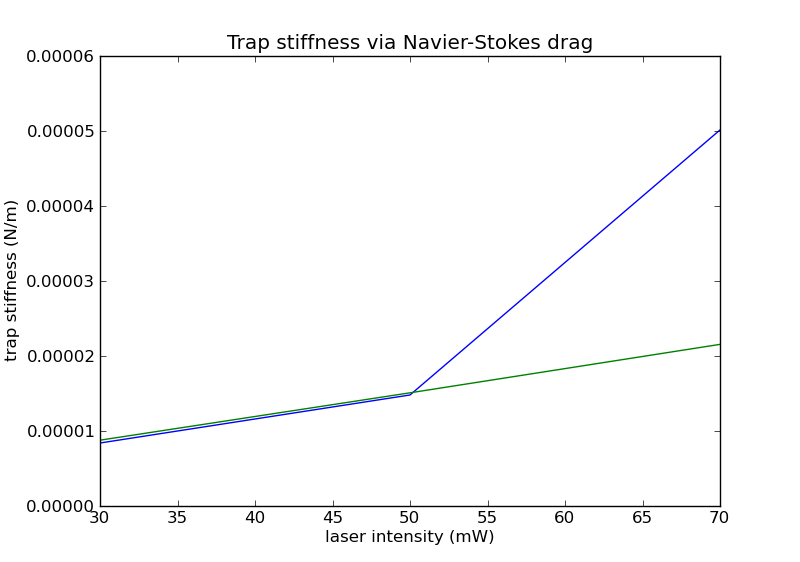
The procedure depicted above is repeated for several laser intensities and for each stage direction.
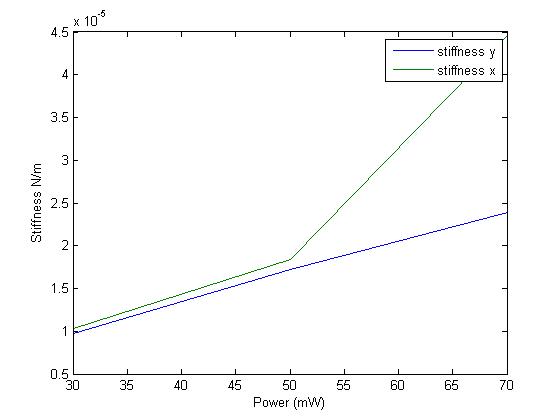
Plot legend: green is stiffness in x and blue is stiffness in y.
The point at 70mW unfortunately breaks the expected linear trend.
Team Lai
Position Calibration
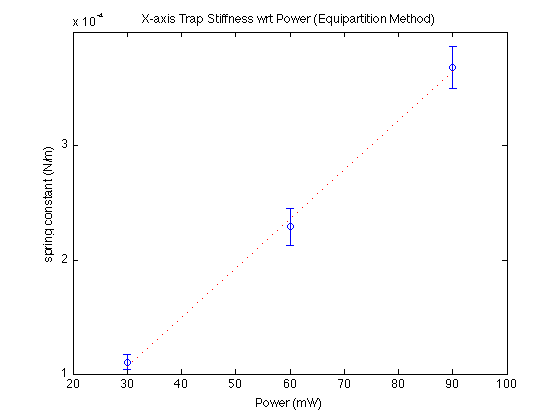
Force Calibrations
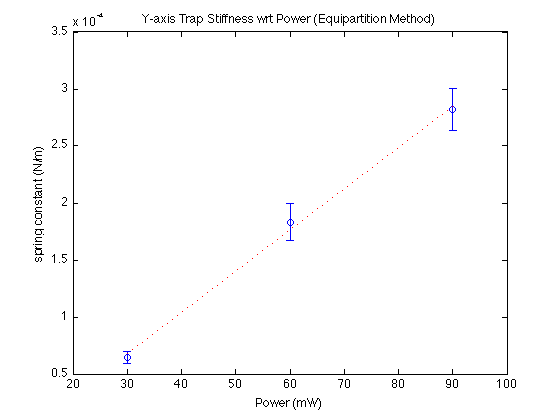
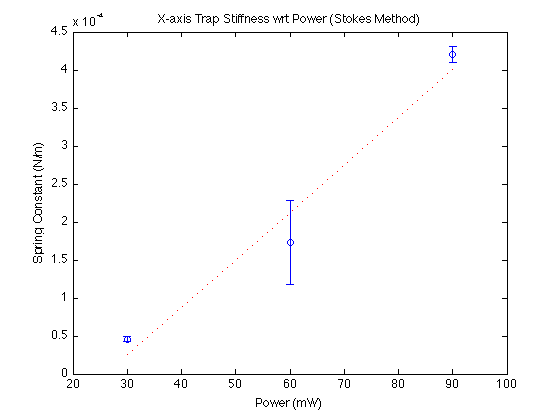
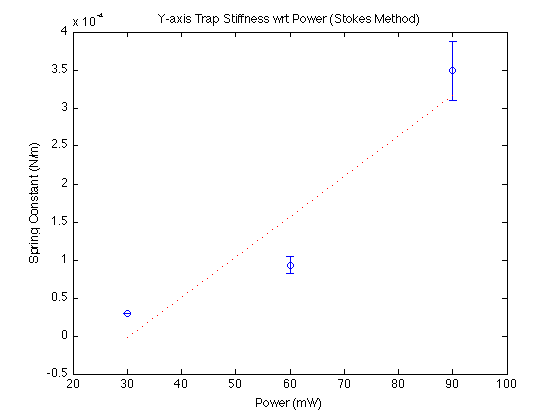
Three measurements taken at 30, 60, 90 mW. Error bars show standard error.