Real electronics
Real electronics sometimes behave significantly different than the idealized models presented in lecture.
Real power supplies
Limits of ideal elements: more realistic model of a battery
Recall the ideal i-v curves for our four elements, referring to Table 1 in the Electronics Primer.
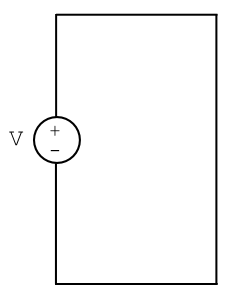
Let’s model a battery as an ideal voltage source connected to no other elements except ideal wires (Fig. 14).
What is the current flowing through this circuit? The resistance of the wires is zero, implying that the current is infinite! Therefore this model, and the associated horizontal i-v curve, is not realistic.
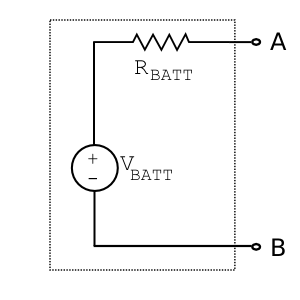
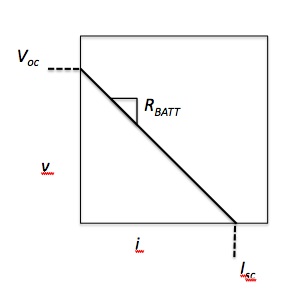
Instead, let’s model the battery as having an internal resistance, $ R_{BATT} $ (Fig. 15). To investigate the i-v curve, we’ll view the output port formed by nodes A and B.
When the port is not connected to anything, resistance is infinite and current is zero. There is no load on the battery, and thus the output voltage at node A must be the full $ V_{BATT} $. This useful quantity is our by now familiar open circuit voltage, $ V_{oc} $.
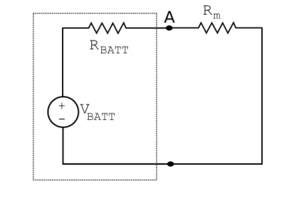
Next, let’s attach a voltmeter to the port with an associated resistance $ R_m $.
When we assume that $ R_m = 0 $, $ v_A $ is shorted to ground. Thus, the current i is at its maximum, namely the short circuit current:
$ I_{sc} = \frac{V_{BATT}}{R_{BATT}} $.
These two quantities define two points on our new, more realistic, i-v curve! Presumably a line connects them, but let’s prove it by solving this simple circuit. We’ll practice our systematic approach once again.
The only unknown node voltage is $ v_A $. The other nodes are either ground or $ V_{BATT} $ by definition of a perfect conductor. Hence we want to solve KCL at $ V_{BATT} $, substituting in the relevant $ v=iR $ constitutive relations:
$ i1 + i2 = 0 = \frac{9-v_A}{R_{BATT}} + \frac{0-v_A}{R_m} = 0 $
and substituting for $ R_m $ using $ I = \frac{v_A}{R_m} $
to simplify to $ v_A = 9-I * R_{BATT} $,
indeed the equation of a line.
From the model diagram, we see that a real battery only sources a full 9V when no load is applied. As current increases, supplied voltage decreases linearly, with negative slope equalling internal resistance. Here is just one simple example of how we can learn about a system by perturbing it -- whether theoretically or experimentally. In this case we found the function relating voltage and current by imagining putting a load on the battery. Note that the equation we found is ultimately not dependent on the resistance of this added load $ R_m $.
Real voltage and current measurement devices
An ideal voltage meter will allow no current to flow through it, but in practice, current can actually flow. A model of an ideal voltage meter includes a circuit element that records the voltage difference between its terminals in series with an infinitely large resistor. In practice, for example in the digital multi-meter (DMM) used in the lab, this series resistor is finite in size, typically on the order of 1 MΩ, and is called the input impedance of the meter. Therefore, if the Thevenin Equivalent resistance of the circuit being measured is also on the order of 1 MΩ then the in-practice model of the DMM must be employed in order to determine the actual output voltage of the circuit if the DMM were not connected. This is generally the desired voltage. An example will demonstrate the difference in behavior between the DMM and the ideal voltmeter.
Real electronic breadboards
At each tie point on the breadboard the connection between the wire or circuit element lead and the internal conductor of the breadboard is not perfect. The imperfection appears as both a parasitic resistance and a parasitic capacitance in series with the circuit element on the breadboard. The resistance can be on the order of 1 Ω while the capacitance can be on the order of a few pF. Thus if the circuit design incorporates capacitance on this order or if the voltage drop caused by a parasitic 1 Ω resistor is relevant, then either these non-idealities must be taken into account or the electronic breadboard must be abandoned in favor of another approach.
Breadboards are most commonly constructed on an anodized metal backboard. The anodization layer is very thin so if a wire or lead is long enough to contact the backboard then it can penetrate that layer and short to the backboard, which may be at ground or at some unknown floating potential.
On the back of the breadboard there are screws holding the banana terminals in place. On new breadboards these are held away from the work surface by rubber or plastic feet on the backboard. On our breadboards these feet have often long since parted company with the backboard. It is wise to cover the screws with a couple layers of electrical tape.
Real capacitors
Real capacitors include a small but sometimes relevant resistance in parallel with the ideal model of a capacitor. This resistance will be specified on the datasheet for the capacitor.
Electrolytic capacitors are generally polarized and cannot support large reverse currents. They should only be used for DC voltages with small AC fluctuations. If they are installed in reverse polarity then at best they will function poorly and start to stink as the rubber cap melts. At worst, they will fail catastrophically and "You'll shoot your eye out" with the metal can that used to contain a capacitor.[1] The negative terminal of the electrolytic capacitor will most often be marked by a thick minus sign (-) or a thick line running the length of the capacitor. Another variation is shown in the image below. Note in the top, axial, electrolytic capacitor the arrows indicate the direction of voltage drop.
Real op-amps
Amplifiers using op-amps unfortunately do not follow the golden rules to the letter. The open-loop gain is not infinite. Therefore the difference between the input voltages is not zero and the current into or out of the inputs is not zero. A realistic model of an op-amp must incorporate a specification for the input offset voltage VOS, an internal voltage that adds to whatever voltage is externally applied to the input terminals V- and V+. The model also incorporates a bias current IB for each input. These are close in real op-amps so the average is specified on the datasheet. However they are not perfectly matched and the difference is specified as the input offset current IOS. All of these non-idealities have the net effect of causing a non-zero voltage, sometimes large, at the output in a negative feedback implementation even when the input is zero. Luckily there are corrective actions available.
Most op-amps provide balance terminals to adjust the output voltage. On the LF411 these are pins 1 and 5. A voltage divider is connected across these terminals with the voltage divider output connected to the negative power terminal, pin 4. The correct divider resistances are not know ahead of time so this balancing act is usually done with a potentiometer, or pot. The pot pins 1 and 3 (the first and last pins) are connected to op-amp pins 1 and 5, while pot pin 2 (the center pin) is connected to op-amp pin 4. It so happens that pots are rather noisy. So once the best balance is achieved with the pot, it can be disconnected and the resistances between pins 1 and 2 and between pins 2 and 3 may be measured. Then the voltage divider can be reconstructed using (high-precision if needed) fixed resistors.
References
- ↑ For more information on why this is a bad thing, please watch A Christmas Story.