Assignment 9, Part 1: model function
Lets get started writing functions to model each physical process that contributes to our DNA melting signal.
Sample temperature
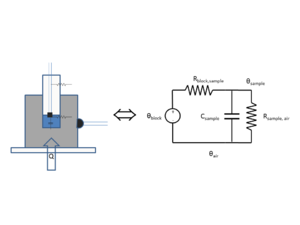
The DNA melter measures the temperature of the metal heating block, not of the sample. Because the glass vial has high thermal resistance, the sample temperature significantly lags the heating block temperature. A simple, lumped-element circuit model can predict the sample temperature to within about 0.5°C based on the block temperature history.
The state variables in a thermal circuit model are temperature T and heat flow q. A fundamental assumption of lumped element models is that each element has a single value of both state variables. Because of this assumption, lumped element models only work well if the bodies you are modeling have a nearly uniform temperature. Components that are small in size, have high thermal conductivity, and have low heat transfer coefficients are most suitable for lumped element modeling. These attributes are summarized by the Biot number, Bi=hl/k, where h is the heat transfer coefficient, l is the characteristic length of the body (volume divided by surface area), and k is the thermal conductivity of the material. Bodies with Biot numbers less than 1 are good candidates for lumped element models. The Biot number for the heating block is on the order of 6x10-3, assuming h=50 W/m2 K, l=3 cm, and k=235 W/m K. This is much less than one, so the heating block is a good candidate for a lumped element model. The Biot number for the glass vial is about 0.03 (h=10.5 W/m2 K, l=3 mm, and k=1.05 W/m K).
The DNA melter measures the heating block's temperature directly. The heating block has a much higher thermal capacity than the sample, so a temperature source is a good model for the block.
The model neglects the heat capacity of the vial.
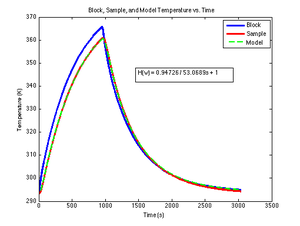
The thermal circuit model for the heating system is shown in the figure on the right. The circuit is a first-order, low-pass filter. In this circuit, a step increase in block temperature causes the sample temperature to rise exponentially to a peak value of Kthermal with time constant τthermal.
The transfer function of the low-pass filter has two parameters:
- $ \frac{\hat{T}_{sample}(\omega)} {\hat{T}_{block}(\omega)}=\frac{K_{thermal}}{j \omega \tau_{thermal} + 1} $.
- Kthermal is the low frequency gain of the system.
- τthermal is the time constant.
Implementation
MATLAB includes several functions for simulating continuous-time, linear, shift-invariant (CTLSI) systems. You can write the transfer function of a CTLSI system as the ratio of two polynomials in $ s $, where $ s=j\omega $. For example, the transfer function of a low-pass filter can be expressed in the form $ H(\omega)=\frac{1}{\tau s+1}=\frac{1}{\tau j \omega+1} $. The MATLAB function tf constructs a software object that represents a CTLSI transfer function. tf takes two arguments that specify the coefficients of the numerator and denominator polynomials. The arguments must be formatted as vectors containing the coefficients of $ s $ in order of decreasing power. For example, the transfer function $ \frac{1}{60 s + 1} $ can be created by:
>> exampleTransferFunction = tf( 1, [ 60 1 ] )
exampleTransferFunction =
1
--------
60 s + 1
Continuous-time transfer function.
Several functions operate on continuous-time transfer function objects. For example bode and impulse generate bode and impulse response plots as expected. (Perhaps the Vice President of Inconsistent Naming at MathWorks was out sick the day those functions were named.) There is also a CTLSI simulator called lsim that will be useful for deriving the sample temperature from the block temperature using a lumped-element model of the thermal low-pass system realized by the heating block, glass vial, and sample. (Seems like the Director of Inconsistencies was back in the office when lsim got named.)
The SimulateLowPass MATLAB function below uses lsim to produce the simulated output of a low-pass filter given its time constant, a vector of input values, and an optional vector of time values. If supplied, the time vector must be the same length as the input vector (i.e. each time value corresponds to one input value). If no time vector is passed, the function generates a time vector assuming that the input values are sampled uniformly at ten times per second, starting at $ t=0 $. The DNA melter software produces ten samples per second.
function SimulatedTemperatureOutput = SimulateLowPass( TimeConstant, InputData, TimeVector )
if( nargin < 3 )
TimeVector = (0:(length(InputData)-1))/10;
end
transferFunction = tf( 1, [TimeConstant, 1] );
initalTemperature = InputData(1);
InputData = InputData - initalTemperature;
SimulatedTemperatureOutput = lsim( transferFunction, InputData, TimeVector' ) + initalTemperature;
end
The function subtracts off the initial value before running the simulation and then adds the initial value back in after the simulation. This is a cheesy way to handle initial conditions — setting the temperature zero point to be equal to the initial temperature. This is equivalent to assuming that the block has been at its initial temperature during the time interval $ t = [ -\infty, 0 ) $.
Save the above function to your MATLAB working directory as SimulateLowPass.m.
Photobleaching
Excited dye molecules can react chemically with compounds in their environment and permanently lose their ability to fluoresce — a phenomenon called photobleaching. LED and ambient light illuminate the LC Green dye for 15 or more minutes over the course of a single melting and annealing cycle, which results in measurable photobleaching. The effect of photobleaching can be approximated by a mathematical model.
Assumptions
- The dye is divided into two populations, bleached and unbleached, with concentrations S and S.
- The initial dye concentration is S + S.
- Only dye molecules bound to dsDNA may be excited.
- Only excited fluorophore molecules bleach.
- An excited fluorophore will either bleach with probability p or return to the ground state with probability 1-p.
- The constant 1-p encompasses all of the mechanisms by which the fluorophore returns to the ground state unbleached, including fluorescence, phosphorescence, and non-radiative relaxation.
- Bleaching is irreversible.
- The number of molecules in the excited state is proportional to fluorescence.
- Bleached and unbleached molecules bind to dsDNA with the same affinity.
Model
Under these assumptions, the bleaching rate is proportional to fluorescence.
- $ \frac{\partial \bar{S}}{\partial t} = K_{bleaching} f(t) $
Kbleaching encompasses several constants, including $ p $, illumination intensity, optical gain of the instrument, and lock-in amplifier gain.
Setting the initial dye concentration to 1, the fraction of unbleached LC Green can be calculated by integrating:
- $ S(t)=1-\bar{S}(t)=1-K_{bleaching}\int_0^t f(t) \mathrm{d}t $
Implementation
A simple way to approximate an integral in discrete time is a cumulative sum: $ \int_0^t f(t) \mathrm{d}t\approx \sum_{n=1}^{t F_s}f(n / F_s) / F_s $, where $ F_s $ is the sample rate. This works particularly well when the signal changes slowly relative to the sample period. It's a good bet that the bleaching time constant is much longer than the 0.1 s sample period. MATLAB has a built-in function for computing cumulative sums called cumsum. Here is an example:
>> cumsum( 1:10 )
ans =
1 3 6 10 15 21 28 36 45 55
cumsum will generate a very good numerical approximation to $ \int_0^t f(t) \mathrm{d}t $.
But what is $ f(t) $ in this case? If you think about it, our model is becoming a bit circular. We are trying to find an expression for the fluorescence as it depends on time and temperature, but we need to already know the fluorescence in order to effectively model photobleaching? Kind of weird... It turns out this stuff happens all the time and we can solve the problem iteratively. That is, we can start with a somewhat-decent guess for $ f(t) $, and use it to calculate a better guess for $ f(t) $. To first-order, we already have a decent guess of the functional form of $ f(t) $ in our expression for $ C_{ds} $. Using the DnaFraction function (available on this page) as a proxy for $ f(t) $ here works relatively well.
function SimulatedBleachingOutput = SimulatePhotobleaching( Kbleach, InputData )
...
end
Thermal quenching
LC Green fluoresces less efficiently at higher temperatures. The decrease in fluorescence is approximately linear. Defining the dye efficiency at the initial temperature to be 1, quenching can be modeled by:
- $ \left . Q(t)=1-K_{quench}[T_{sample}(t)-T_{sample}(0)]\right . $
function SimulatedQuenchingOutput = SimulateThermalQuenching( Kquench, InputData )
...
end
Instrument gain and offset
There are several optical and electronic gain factors built into the DNA melter that determine the instrument responsively, ∂Vf,measured / ∂ Cds. In addition, Vf,measured may be offset from zero when Cds concentration is zero.
- Kgain is equal to the change in Vf,measured divided by the change in fraction of dsDNA. This is assumed to be constant.
- Koffset is equal to the value of Vf,measured when the dsDNA concentration is zero.
Expression for model Vf,model
Once you have all the pieces, put everything together into a single model function representing:
- $ \left . V_{f,model}(t) = K_{gain} S(t) Q(t) C_{ds}(T_{sample}(t), \Delta H^\circ, \Delta S^\circ) + K_{offset}\right . $
Here, Cds is the model melting curve produced by the DnaFraction function from Assignment 7.
| |
Write a MATLAB function representing Vmodel that takes in all the necessary parameters, as well as the block temperature, and outputs the modeled fluorescence. |
function SimulatedOutput = Vfmodel( Kgain, Koffset, ... , BlockTemperature )
...
end
- Assignment 9 Overview
- Part 1: model function
- Part 2: test your code with simulated data
- Part 3: fitting your data