20.309: Biological Instrumentation and Measurement

The following two tables will pop up frequently in 20.309 for the rest of the semester. Table 8.0.1 describes the Fourier transform and many of its useful properties, while table 8.0.2 contains the transform pairs of many common functions. These two tables are useful because you can combine functions in table 8.0.2 using the properties in table 8.0.1 to figure out the transforms of an endless number of functions (without doing any math!).
Note: there is an error in the table below. The transform of $ u(t) $ is: $ \frac{1}{2}\left ( \frac{1}{i \pi f}+\delta (f) \right ) $.
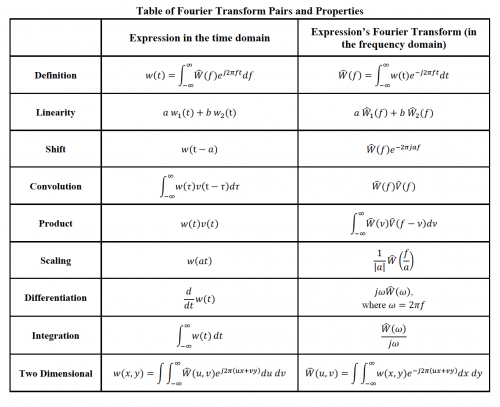
Table 8.0.1: Short table of Fourier transform properties 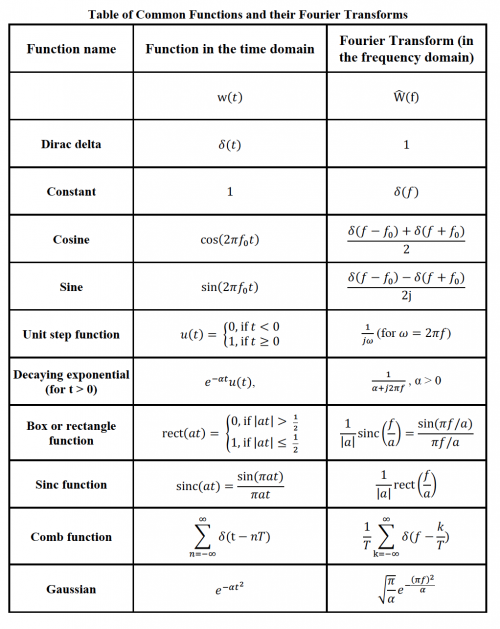
Table 8.0.2: Short table of Fourier transform pairs

|
- Sketch each function in table 8.0.2 as well as the magnitude of its Fourier transform. Include any relevant constants in your sketch (for example: a, $ \alpha $, and $ f_0 $).
-
In class we found the Fourier transform of $ \cos^2(\omega_0 t) $. Use graphical convolution to determine the transform of $ \cos^4(\omega_0 t) $.
-
Using the transform pairs in table 8.0.2, sketch the fourier transform of $ e^{-\alpha t} u(t) \times \cos(\omega_0 t) $. Assume that $ \alpha\ll\omega_0 $.
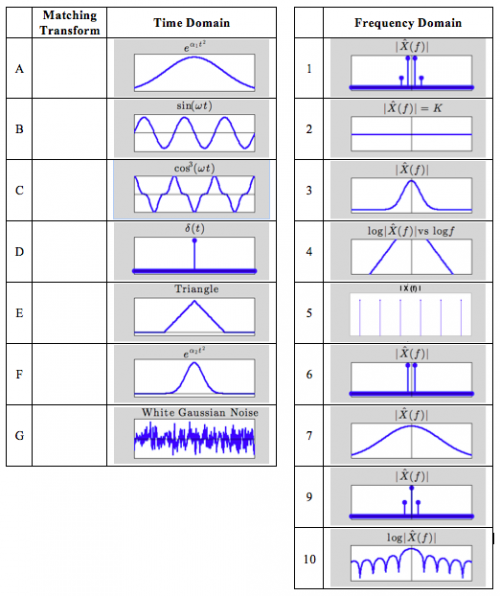
- Table 8.0.3 shows plots of eight time-domain signals A-H. The table on the right includes magnitude plots of the Fourier transform of ten signals numbered 1-10. For each time domain signal A-H, write the number 1-10 in the empty column of the matching frequency-domain signal. You may use a numbered plot more than once.
Some of the frequency plots are shown on log-log axes and some are linear, as indicated by the plot title.
Hint: Gaussian or white noise is a random signal with equal contributions from every frequency.
|
Navigation
Back to 20.309 Main Page