20.109(S21):M3D3
Contents
Introduction
To test the effects of the mutations in the Variant IPC proteins, we will revisit several concepts that were discussed in Mod1. Specifically, a titration curve is used to calculate $ K_d $ of IPC binding to calcium! As a review, consider the simple case of a receptor-ligand pair that are exclusive to each other, and in which the receptor is monovalent. The ligand (L) and receptor (R) form a complex (C), which can be written
$ R + L \rightleftharpoons\ ^{k_f}_{k_r} C $
At equilibrium, the rates of the forward reaction (rate constant = $ k_f $) and reverse reaction (rate constant = $ k_r $) must be equivalent. Solving this equivalence yields an equilibrium dissociation constant $ K_d $, which may be defined either as $ k_r/k_f $, or as $ [R][L]/[C] $, where brackets indicate the molar concentration of a species. Meanwhile, the fraction of receptors that are bound to ligand at equilibrium, often called y or θ, is $ C/R_{TOT} $, where $ R_{TOT} $ indicates total (both bound and unbound) receptors. Note that the position of the equilibrium (i.e., y) depends on the starting concentrations of the reactants; however, $ K_d $ is always the same value. The total number of receptors $ R_{TOT} $= [C] (ligand-bound receptors) + [R] (unbound receptors). Thus,
$ \qquad y = {[C] \over R_{TOT}} \qquad = \qquad {[C] \over [C] + [R]} \qquad = \qquad {[L] \over [L] + [K_d]} \qquad $
where the right-hand equation was derived by algebraic substitution. If the ligand concentration is in excess of the concentration of the receptor, [L] may be approximated as a constant, L, for any given equilibrium. Let’s explore the implications of this result:
- What happens when L << $ K_d $?
- →Then y ~ $ L/K_d $, and the binding fraction increases in a first-order fashion, directly proportional to L.
- What happens when L >> $ K_d $?
- →In this case y ~1, so the binding fraction becomes approximately constant, and the receptors are saturated.
- What happens when L = $ K_d $?
- →Then y = 0.5, and the fraction of receptors that are bound to ligand is 50%. When y = 0.5, the concentration of free calcium (our [L]) is equal to $ K_d $.
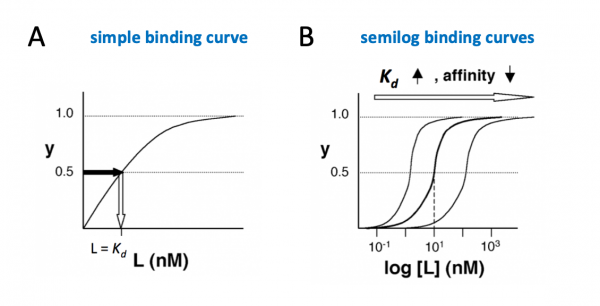
The figures below demonstrate how to read $ K_d $ from binding curves:
Simple binding curve
The binding fraction y at first increases linearly as the starting ligand concentration is increased, then asymptotically approaches full saturation (y=1). The dissociation constant $ K_d $ is equal to the ligand concentration [L] for which y = 1/2.
Semilog binding curves
By converting ligand concentrations to logspace, the dissociation constant is readily determined from the inflection point of the sigmoidal curve. The three curves each represent different ligand species. The middle curve has a $ K_d $ close to 10 nM, while the right-hand curve has a higher $ K_d $ and therefore lower affinity between ligand and receptor (vice-versa for the left-hand curve).
Because inverse pericam has multiple binding sites the IPC-calcium binding is more complicated than the example above. The $ K_d $ reported in the IPC reference article by Nagai et. al. is called an ‘apparent $ K_d $’ because it reflects the overall avidity of multiple calcium binding sites, not their individual affinities for calcium. Normally, calmodulin has a low affinity (N-terminus) and a high affinity (C-terminus) pair of calcium binding sites. However, the E104Q mutant, which is the version of CaM used in inverse pericam, displays low affinity binding at both termini. Moreover, the Hill coefficient, which quantifies cooperativity of binding in the case of multiple sites, is reported to be 1.0 for inverse pericam. This indicates that inverse pericam behaves as if it were binding only a single calcium ion per molecule. Thus, wild-type IPC is well-described by a single apparent $ K_d $.
For any given variant IPC, things may be more complicated. Keep in mind that we are not directly measuring calcium binding, but instead are indirectly inferring it based on fluorescence. A change in fluorescence requires the participation not only of calcium, but also of M13. In addition to the four separate calcium binding sites in calmodulin, the M13 binding site influences apparent affinity and apparent cooperativity. In short, be careful about how you describe the meanings of our binding parameters in your data analysis.
Protocols
Part 1: Participate in Comm Lab workshop
Our communication instructors, Dr. Prerna Bhargava and Dr. Sean Clarke, will join us today for a discussion on preparing a Research proposal presentation.
Part 2: Prepare samples for titration curve
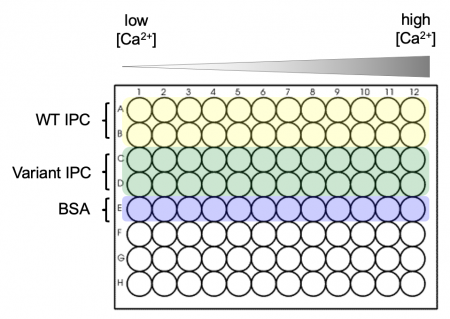
- Obtain a black 96-well plate and review the plate map schematic at right: the top two rows will be loaded with WT IPC, the next two rows will be loaded with your Variant IPC, and the final row will be loaded with BSA.
- BSA will be used to measure the background signal.
- A black plate is used to minimize "cross-talk" (i.e., light leakage) between samples in adjacent wells.
- Aliquot the WT IPC protein into the appropriate wells of the plate.
- Add 30 μL of the purified protein to each well in rows A and B.
- Aliquot the Variant IPC protein into the appropriate wells of the plate.
- Add 30 μL of the purified protein to each well in rows C and D.
- Aliquot 30 μL of 0.1% BSA to each of the wells in row E.
- The calcium solutions are at the front bench in reservoirs that will be shared across the class.
- Carefully carry your plate to the front bench to add these solutions.
- From shared reservoir #1 (calcium concentration = 0 nM), use the multi-channel pipet to add 30 μL to the top five rows in the first column of the plate. Discard the pipet tips.
- Work from reservoirs #2 to #12 (lowest calcium concentration to highest calcium concentration), and from the left-hand to the right-hand columns on your plate.
- Be sure to use fresh pipet tips each time! If you do contaminate a solution, let the Instructor know so the solution can be replaced. Honesty about a mistake is far preferred here to affecting every downstream experiment.
- When you are done, alert the Instructor and you will be taken in small groups to measure the fluorescence values for your samples.
- Samples will be measured using a platereader.
- Settings included an excitation wavelength of 485 nm and an emission wavelength at 515 nm.
In your laboratory notebook, complete the following:
- Recall your analysis of the SDS-PAGE and microBCA completed on M3D1. Were the Variant IPC and WT IPC concentrations consistent / similar across each of the purified protein samples?
- Given that the same volume is added to each the titrations completed with each of Variant IPC and WT IPC (30 µL of each purified protein sample was added), might this impact the results from the titration curve experiment? How?
- What change(s) could be made to the protocol to ensure the same amount of Variant IPT or WT IPC was used in each titration curve experiment? Be specific on how you might address this issue.
Part 3: Analyze titration curve data
You will analyze your calcium titration assay data in two steps. First, you will get a rough sense for how the mutations changed (or didn't) binding activity compared to WT IPC by plotting the averages of the two replicate values for each Variant IPC, in both raw and processed form. Second, you will take the average processed values and use MATLAB code that will more precisely determine the affinity and cooperativity for the Variant IPC and WT IPC with respect to calcium.
The spreadsheet with the data that will be used for the analysis is linked here. In this spreadsheet, the fluorescence measurements for duplicate samples of WT IPC and each of the Variant IPC are provided. The calcium concentrations (nM) are listed across the top of the spreadsheet.
Plot titration curve in Excel to determine first estimate of Kd
Today you will analyze the fluorescence data for the WT IPC and six Variant IPC. First, you will use Excel to visualize the raw data. In addition, you will normalize the data to prepare for more advanced analysis using MATLAB.
- Open the Excel file linked above.
- In column A the samples that were measured are listed. Because duplicates of each sample were measured, two values are provided in the table for the WT IPC and each Variant IPC.
- The calcium concentrations (nM) are provided in the top row.
- Review the data provided in the Excel spreadsheet.
- In your laboratory notebook, complete the following:
- Do the numbers make sense? Remember that IPC fluorescence decreases when calcium is bound.
- Are there any anomalies in the data (does anything appear strange / unexpected)?
- Begin by calculating the averages for the duplicate samples.
- To visualize the raw data, plot the averages for each sample (y-axis) as a function of calcium concentration (x-axis). Be sure to change the x-axis to a log scale.
- In your laboratory notebook, complete the following:
- Include the plot of the raw data.
- Briefly describe how each Variant IPC differs from the WT IPC.
- Next you will normalize the data to the 0 nM calcium fluorescent value for each sample by converting all values to a percent.
- Because the fluorescence measured at 0 nM calcium for each sample will be used to normalize the data, create a new table in the Excel spreadsheet containing each of the samples wherein this value will be set to "1".
- In the new table, each sample should be listed in the first column (as in the original spreadsheet) and the value for 0 nM calcium should be entered as "1" for each sample.
- This means that the fluorescence value measured for each of the samples at 0 nM calcium is now set at 100% in your data analysis.
- To calculate the % fluorescence for the remaining calcium concentrations, divide by the fluorescence value measured for the 0 nM calcium condition.
- For example, if the 0 nM calcium fluorescence value for the WT IPC equals 1200, then the fluorescence values measured for calcium concentrations 8.5 nM through 19.5 µM should be divided by 1200.
- This normalized value represents the % fluorescence for each calcium concentration based on the value at 0 nM calcium for each sample.
- To visualize the normalized data, plot the % fluorescence values for each sample (y-axis) as a function of calcium concentration (x-axis). Be sure to change the x-axis to a log scale.
- In your laboratory notebook, complete the following:
- Include the plot of the normalized data.
- Briefly describe how each Variant IPC differs from the WT IPC.
- Does this plot look similar or different from the plot of the raw data?
- Can you estimate the Kd from the binding curves in either the raw or normalized data plots?
Use MATLAB modeling to estimate Kd
Next you will use the normalized data generated above to determine the Kd by fitting the data to a curve in MATLAB.
- Create a folder in MATLAB and upload the following scripts: F15_Fit_Main, Fit_SingleKD, and Fit_KDn
- In MATLAB, open the folder with the above files then double-click on 'F15_Fit_Main'.
- Read through the script, particularly the introductory comments (indicated by the % sign) to learn more about what is accomplished by each step in the code.
- If you encounter unfamiliar terms, return to the workspace and type help functionname for a description of the command.
- Place your cursor at line 1 and click to highlight the first section of the code.
- Click 'Run section'.
- This will clear the workspace such that parameters set previously do not interfere with the analysis.
- Enter the normalized fluorescence values for the WT IPC, Variant #1 IPC, and Variant #2 IPC where indicated.
- Currently placeholder values are entered. Simply delete the placeholder values and enter your data.
- Place your cursor at line 10 and click to highlight the section of code.
- Click 'Run section' to execute the code.
- The functions in this section will calculate the binding fractions from the fluorescence data entered.
- In your laboratory notebook, complete the following:
- Consider the equation used in the MATLAB code to calculate fraction bound. How does fraction bound relate to the fluorescence values measured?
- Why is it necessary to use the fraction bound (rather than the fluorescence data) in determining the Kd?
- Place your cursor at line 35 and click to highlight Part 1: Fit for single Kd value using a simple model.
- This script uses the nonlinear fitting tool to determine Kd values according to the model defined in 'Fit_SingleKD', which ignores multiple ligand sites and provides a simplified representation of binding.
- Click 'Run section' to execute the code.
- Examine the graphs (Figure 1 and Figure 2) generated in MATLAB.
- Figure 1 includes graphs for the WT IPC and each Variant IPC wherein the data points and model curves are displayed.
- Figure 2 is a graph displaying the residuals, or difference between the data and the model, of the WT IPC and each Variant IPC. If the absolute values are low, this indicates good agreement between the model and the data numerically. Whether or not this is the case, another thing to look for is whether the residuals are evenly and randomly distributed about the zero-line. If there is a pattern to the errors, likely there is a systematic difference between the data and the model, and thus the model does not reflect the actual binding process well.
- Examine the Kd values that were calculated using this model.
- These values should be present in the Command Window.
- In your laboratory notebook, complete the following:
- Include all graphs.
- Record the Kd values.
- How do the graphs generated in Figure 1 compare to the graph you plotted in Excel?
- What does the residuals graph tell you about the fit of your data to the model?
- Place your cursor at line 108 and click to highlight Part 2: Model for single Kd plus Hill coefficient, Method 1.
- This script uses a function that more appropriately represents the binding behavior of IPC according to the model defined in 'Fit_KDn', which allows for multiple binding sites and tests for cooperativity among them. The parameter used to measure cooperativity is called the Hill coefficient. A Hill coefficient of 1 indicates independent binding sites, while greater or lesser values reflect positive or negative cooperativity, respectively.
- Click 'Run section' to execute the code.
- Examine the graphs (Figure 3 and Figure 4) generated in MATLAB.
- Figure 3 includes graphs for the WT IPC and each Variant IPC wherein the data points and model curves are displayed.
- Figure 4 is a graph displaying the residuals.
- In your laboratory notebook, complete the following:
- Include all graphs.
- Record the Kd values and Hill coefficients.
- Which model appears to better fit the WT IPC data (consider Figure 1 vs Figure 3 AND Figure 2 vs Figure 4)? The Variant IPC data?
- Part 3: Model for single Kd plus Hill coefficient, Method 2 is entirely optional if you are interested in another function available for defining Kd and Hill coefficient.
- If you choose to use this script, be sure to update the range of the linear transition region for each sample.
- Lastly, analyze your data using a model able to account for two $ K_d $ values.
- Upload the following scripts to your MATLAB folder: Fit_TwoKD and Fit_TwoKD_Func
- Double-click on 'Fit_TwoKD'.
- Read through the script, then then enter the normalized fluorescence values for the WT IPC where indicated. Note: in this script only one sample can be analyzed at a time!
- Currently placeholder values are entered. Simply delete the placeholder values and enter your data.
- Click 'Run' to execute the code.
- Examine the graph that was generated in MATLAB.
- Examine the output values that were calculated using this model.
- In your laboratory notebook, complete the following:
- Include all graphs.
- Record the f, Kd, and n values. What do the f and n values represent?
- Of all of the models examined, which best represents the WT IPC binding data?
- To complete the data analysis for all of the Variant IPC, complete the above steps such that each Variant IPC is analyzed using the models included at Steps #9, #14, and #19. You can do this by simply running the code in multiple rounds such that each Variant IPC is analyzed or, if you are comfortable with the code, you can edit the script such that all samples can be analyzed together.
- In your laboratory notebook, complete the following:
- Include all graphs and data for each Variant IPC.
- Describe how each mutation altered binding and / or cooperativity of the Variant IPC compared to WT IPC.
Next day: Design new IPC variant