|
|
| Line 68: |
Line 68: |
| | [[File:Transfer function matching pole zero plots.png|700 px]] | | [[File:Transfer function matching pole zero plots.png|700 px]] |
| | </center> | | </center> |
| | + | {{Template:Assignment Turn In|message = |
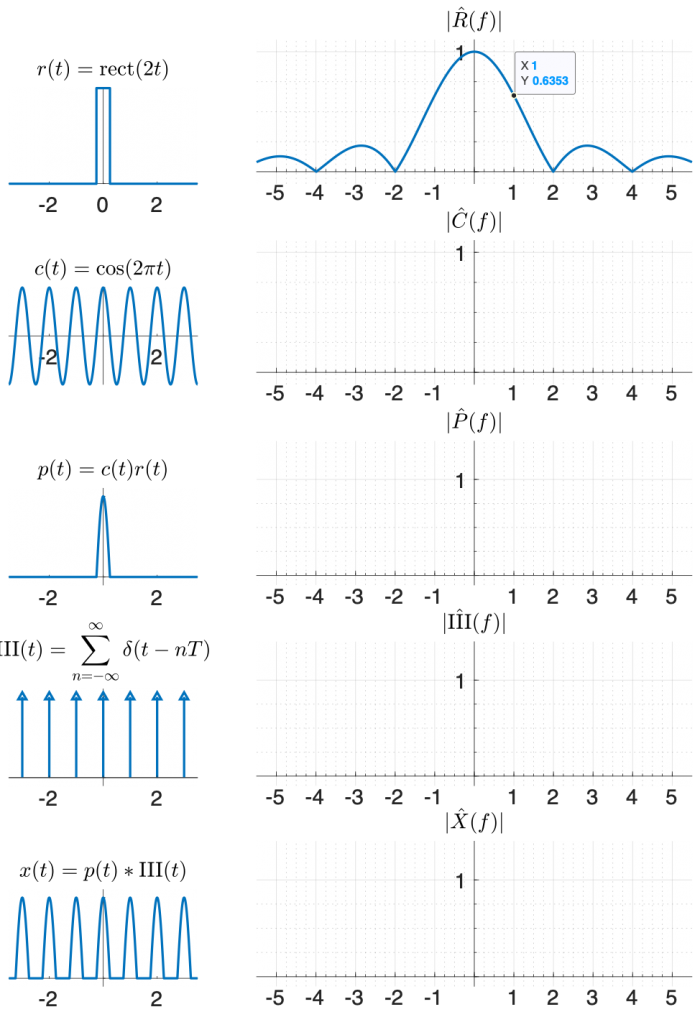
| | + | * Use graphical methods to find the Fourier transform of the half-cosine pulse function x(t) plotted below, which consists of the positive half of a 1 Hz cosine, repeated forever at a rate of 1 Hz. |
| | + | * What is the lowest frequency component of x(t), not counting <math>\hat{X}(0)</math>? |
| | + | }} |
| | + | |
| | + | [[File:Cosine pulse function.png|700 px]] |
| | + | One way to create x(t) using functions that appear on the transform table is: |
| | + | # '''multiply''' a '''cosine''' by a '''rectangle''', and then |
| | + | # '''convolve''' the result with the '''comb function''' <math>\mathrm{III(}t)=\sum\limits_{n=-∞}^{∞} \delta(t-nT)</math>. |
| | + | Use the diagram below to help you find the answer. The left column of shows signals in the time domain, and the right column shows the magnitude of the Fourier transform of each signal. The top right plot is filled in for you, plus a little hint that might help you make an accurate plot. |
| | + | |
| | + | (The phase of the transforms in this problem is zero at all frequencies, so it is not plotted.) |
| | + | |
| | + | [[File:Cosine pulse transform worksheet.png|700 px]] |
| | | | |
| | ==Feedback systems== | | ==Feedback systems== |
Revision as of 03:05, 27 April 2020
20.309: Biological Instrumentation and Measurement

Signals and systems

|
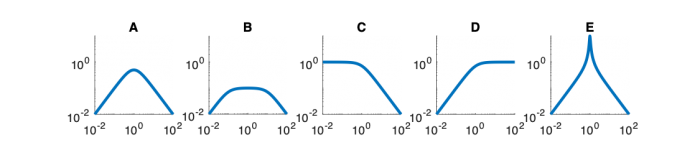
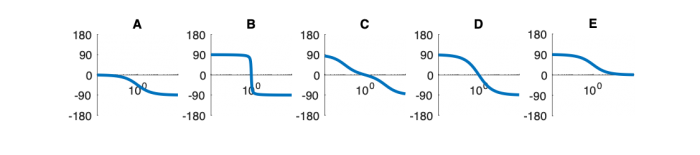
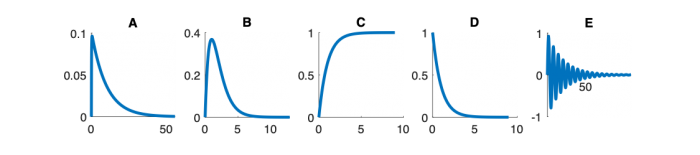
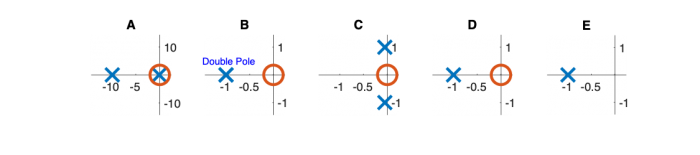
Fill out the table below. Match each system function with its Bode magnitude and phase plot, step response, and pole zero diagram. (Write one letter A-E in each box below.) In the row labeled “Description,” write a descriptive name of each system, such as “low-pass filter” or “overdamped second-order system.”
|
| System function
|
$ \frac{1}{s+1} $
|
$ \frac{s}{s+1} $
|
$ \frac{s}{s^2+2s+1} $
|
$ \frac{s}{s^2+0.1s+1} $
|
$ \frac{1}{s^2+10s+1} $
|
| Magnitude plot
|
|
|
|
|
|
| Phase plot
|
|
|
|
|
|
| Step response
|
|
|
|
|
|
| Pole/zero plot
|
|
|
|
|
|
| Description
|
|
|
|
|
|
Magnitude Plots
Phase Plots
Step Response Plots
Pole Zero Plots

|
- Use graphical methods to find the Fourier transform of the half-cosine pulse function x(t) plotted below, which consists of the positive half of a 1 Hz cosine, repeated forever at a rate of 1 Hz.
- What is the lowest frequency component of x(t), not counting $ \hat{X}(0) $?
|
 One way to create x(t) using functions that appear on the transform table is:
One way to create x(t) using functions that appear on the transform table is:
- multiply a cosine by a rectangle, and then
- convolve the result with the comb function $ \mathrm{III(}t)=\sum\limits_{n=-∞}^{∞} \delta(t-nT) $.
Use the diagram below to help you find the answer. The left column of shows signals in the time domain, and the right column shows the magnitude of the Fourier transform of each signal. The top right plot is filled in for you, plus a little hint that might help you make an accurate plot.
(The phase of the transforms in this problem is zero at all frequencies, so it is not plotted.)
Feedback systems

|
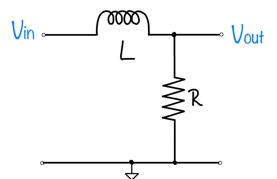
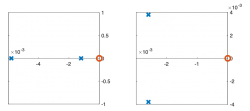
- Find the transfer function H ̂(s)=(V ̂_out (s))/(V ̂_in (s)) of the circuit shown below, assuming L = 1 H and R = 1Ω.
- Plot the poles and zeros of H ̂(s) on the axes below using x’s for poles and o’s for zeroes.
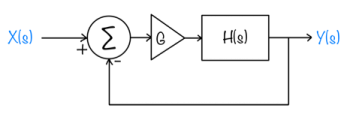
- The circuit from Figure 1 is placed in a feedback system, as shown in the block diagram below. The triangle represents an amplifier with gain G that does not depend on frequency. Find the transfer function of the feedback system $ \hat{F}(s)=(\hat{Y}(s))/(\hat{X}(s)). $
- Plot the poles and zeros of $ \hat{F}(s) $ for G=1,9,and 19. Label the gain value for each point.</math>
|

|
- Find the transfer function of the circuit below for L = 1 H and R = 1 Ω and C=1 F.
- The circuit is placed in the same feedback system shown in the previous question. Plot the poles for gains of 1/4, 3/4, 5/4, 10/4, and 17/4. You may generate your plot by hand or use MATLAB.
|

The Frequency Dependence of Osmo-Adaptation in Saccharomyces cerevisiae

|
Read The Frequency Dependence of Osmo-Adaptation in Saccharomyces cerevisiae and the supporting information.. This paper will be the focus of exam 2. We will discuss the paper and the supporting information on Thursday and Friday.
Answer the following questions about The Frequency Dependence of Osmo-Adaptation in S. cerevisiae:
- What is the primary mechanism by which S. cerevisiae recovers from hyperosmotic shock?
- What mathematical model did Mettetal, et. al. use for Hog1 activation in response to a hyperosmotic shock? Express the model in the following forms
- transfer function (TF)
- poles and zeros (ZPK)
- single differential equation (SDE)
- coupled differential equations (CDE)
Express the TF, SDE, and ZPK models in terms of the undamped natural frequency, $ \omega_0 $, damping ratio $ \zeta $, and/or damped natural frequency $ \omega_D $.
- What mathematical model did Mettetal, et. al. use to account for nonlinearities in the system?
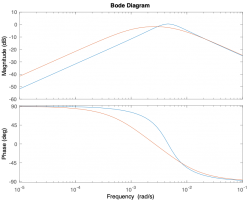
- Plot the frequency response (i.e. make a Bode plot) of the model over a range of $ \omega_0 $ and $ \zeta $ values that includes over damped, critically damped, and under damped.
- Find an expression for the step response and plot it over a range of values of $ \omega_0 $ and $ \zeta $. A hand-drawn plot is fine, but you should probably look into MATLAB's step function.
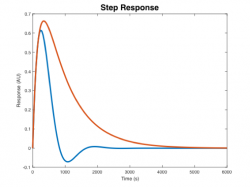
- Mettetal, et. al. found that that the hyperosmotic shock response of wild-type yeast was (choose one): underdamped, critically damped, or overdamped.
- The response of the mutant (low Pbs) yeast was (choose one): underdamped, critically damped, or overdamped.
- Which of the step responses below corresponds to Mettetal's model for the wild-type strain and the mutant strain (neglecting the nonlinear element).
- Which of the Bode plots below corresponds to Mettetal's model for the wild-type strain and the mutant strain.
- Which of the pole zero diagrams below corresponds to Mettetal's model for the wild-type strain and the mutant strain.
- What are two questions that you have about the paper's methodology?
</div>
|
</div>
 One way to create x(t) using functions that appear on the transform table is:
One way to create x(t) using functions that appear on the transform table is: