Difference between revisions of "Spring 2020 Assignment 9"
From Course Wiki
(→The Frequency Dependence of Osmo-Adaptation in Saccharomyces cerevisiae) |
(→The Frequency Dependence of Osmo-Adaptation in Saccharomyces cerevisiae) |
||
| Line 108: | Line 108: | ||
{| | {| | ||
|[[file:Mettetal yeast model step response.png|250 px]] | |[[file:Mettetal yeast model step response.png|250 px]] | ||
| − | + | |[[file:Mettetal yeast model Bode plots.png|250 px]] | |
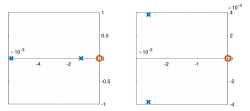
| − | + | |[[file:Mettetal yeast model pole zero diagrams.png|250 px]] | |
|} | |} | ||
</center> | </center> | ||
{{Template:20.309 bottom}} | {{Template:20.309 bottom}} | ||
Revision as of 20:30, 26 April 2020
Signals and systems
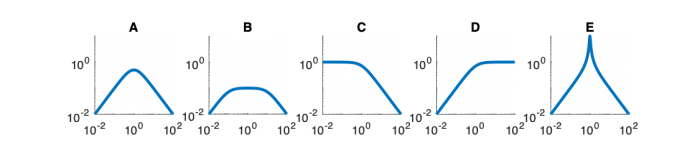
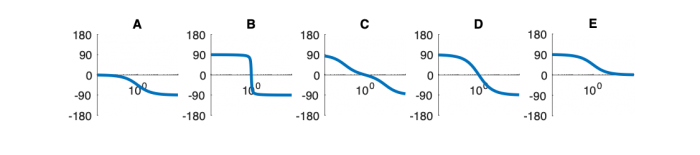
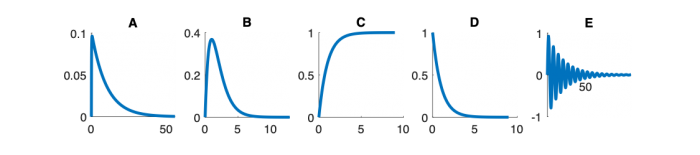
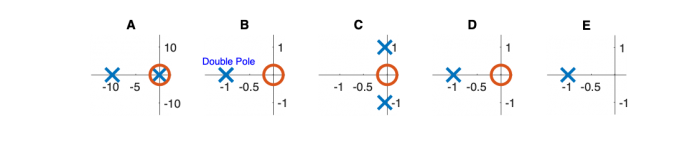
| System function | $ \frac{1}{s+1} $ | $ \frac{s}{s+1} $ | $ \frac{s}{s^2+2s+1} $ | $ \frac{s}{s^2+0.1s+1} $ | $ \frac{1}{s^2+10s+1} $ |
|---|---|---|---|---|---|
| Magnitude plot | |||||
| Phase plot | |||||
| Step response | |||||
| Pole/zero plot | |||||
| Description |
Magnitude Plots
Phase Plots
Step Response Plots
Pole Zero Plots
Feedback systems
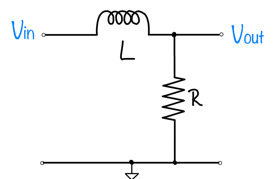
|
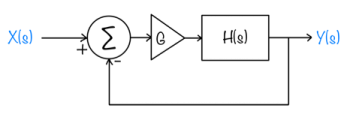
|
The Frequency Dependence of Osmo-Adaptation in Saccharomyces cerevisiae
| |
Read The Frequency Dependence of Osmo-Adaptation in Saccharomyces cerevisiae and the supporting information.. This paper will be the focus of exam 2. We will discuss the paper and the supporting information on Thursday and Friday. Answer the following questions about The Frequency Dependence of Osmo-Adaptation in S. cerevisiae:
</div> |
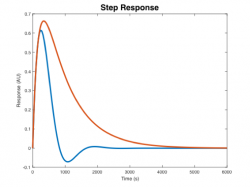
|
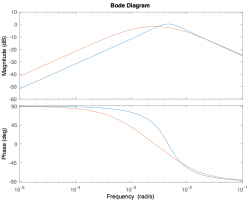
|
|