Difference between revisions of "Nonlinear regression"
(→Review of linear regression) |
|||
| Line 12: | Line 12: | ||
==Review of linear regression== | ==Review of linear regression== | ||
| − | Linear Regression is a method for finding the magnitude of the relationship between two variables that co-vary. The technique assumes that a straight line characterizes the relationship between the two quantities: 𝑦=𝛽𝑥+𝛼, where 𝛽 is the true slope and 𝛼 is the true intercept. | + | Linear Regression is a method for finding the magnitude of the relationship between two variables that co-vary. The technique assumes that a straight line characterizes the relationship between the two quantities: 𝑦=𝛽𝑥+𝛼, where 𝛽 is the true slope and 𝛼 is the true intercept. A simple way to find <i>α</i> and <i>β</i> is to measure the <i>y</i> at two different values of <i>x</i>, giving the datapoints <span style="white-space: nowrap;">(<i>x<sub>i</sub></i>, <i>y<sub>i</sub></i>); <i>i</i> = {1,2}</span>. If the two points are precisely known, solving for the exact values of 𝛼 and 𝛽 is trivial. Unfortunately, all physical measurements include noise. The presence of noise precludes finding the exact values of 𝛼 and 𝛽. |
| − | + | Measurement noise can be modeled by adding a noise term, <i>ε<sub>i</sub></i>, to the right side of the model equation: <i>y<sub>i</sub></i>=<i>Β<sub>i</sub>x</i>+<i>α</i>+<i>ε<sub>i</sub>x</i>. The function of linear regression is to produce estimates of 𝛼 and 𝛽, denoted by <i>α̂</i> and <i>β̂</i>, from a sample of N value pairs <span style="white-space: nowrap;">(<i>x<sub>i</sub></i>, <i>y<sub>i</sub></i>); <i>i</i> = {1, ..., N}</span> that includes noise in the <i>y</i>-values. The most common regression model assumes that x is known exactly. In practice, regression works well if the relative magnitude of noise in <i>x</i> is much smaller than <i>y</i>. | |
| Line 41: | Line 41: | ||
* plot 'em for an informal look | * plot 'em for an informal look | ||
* various tests of residuals exist | * various tests of residuals exist | ||
| − | |||
==Overview of nonlinear regression== | ==Overview of nonlinear regression== | ||
Revision as of 18:55, 5 January 2013
… the safe use of regression requires a good deal of thought and a good dose of skepticism
Review of linear regression
Linear Regression is a method for finding the magnitude of the relationship between two variables that co-vary. The technique assumes that a straight line characterizes the relationship between the two quantities: 𝑦=𝛽𝑥+𝛼, where 𝛽 is the true slope and 𝛼 is the true intercept. A simple way to find α and β is to measure the y at two different values of x, giving the datapoints (xi, yi); i = {1,2}. If the two points are precisely known, solving for the exact values of 𝛼 and 𝛽 is trivial. Unfortunately, all physical measurements include noise. The presence of noise precludes finding the exact values of 𝛼 and 𝛽.
Measurement noise can be modeled by adding a noise term, εi, to the right side of the model equation: yi=Βix+α+εix. The function of linear regression is to produce estimates of 𝛼 and 𝛽, denoted by α̂ and β̂, from a sample of N value pairs (xi, yi); i = {1, ..., N} that includes noise in the y-values. The most common regression model assumes that x is known exactly. In practice, regression works well if the relative magnitude of noise in x is much smaller than y.
The most common type of LR minimizes the value of the squared vertical distances between observed and predicted values
Model :
Assumptions:
the independent variable 𝑥 is known with certainty (or at least very much less error than 𝑦)
𝜀 is an independent, random variable with 𝜇=0
The distribution of 𝜀 is symmetric around the origin
the likelihood of large errors is less than small ones
Uncertainty in slope estimate
The error in slope 𝑊=𝛽 ̂−𝛽
Variance of 𝑊 characterizes slope error
You can calculate a 95% (or other significance level) confidence interval for 𝛽 ̂
What factors should the uncertainty depend on?
Estimate 𝜎^2 (𝑊): 𝑉^2 (𝑊)=(∑▒〖𝑟_𝑖^ 〗^2 )/((𝑁−2)∑▒〖(𝑥_𝑖−𝑥 ̅)〗^2 )
N-2 is a “penalty” because regression line minimizes variance of residuals
If the interval contains 0, the null hypothesis that 𝛽=0 cannot be rejected
Step 1: PLOT THE DATA
Examine the residuals
- plot 'em for an informal look
- various tests of residuals exist
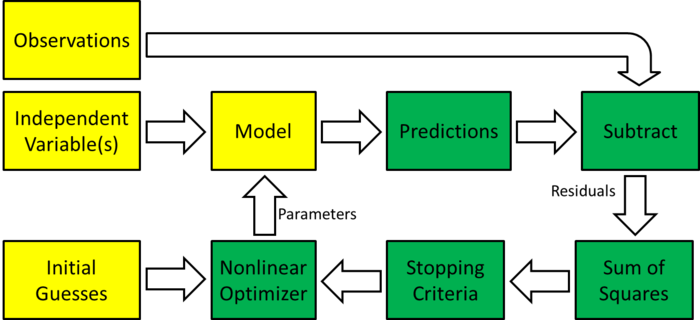
Overview of nonlinear regression
| Block diagram of nonlinear regression |