Geometrical optics and ray tracing
Overview
Light is an extraordinarily complicated, three dimensional, time dependent phenomenon. There are two predominant theoretical models of light: the wave (or classical) theory and the quantum theory. In the wave theory, light is modeled as a time-varying electric and magnetic field. Completely describing a light field requires specifying the intensity, phase, and direction of the electric and magnetic field at every point in space and time. In the quantum model, light is composed of discrete energy packets with probabilistic behavior. Neither model makes it particularly easy to conceptualize how a pair of binoculars or a microscope works. Fortunately, there is a simplified model of light called ray optics that works well in situations where the objects that interact with a light field are much larger than the wavelength of the light. Ray optics (also called geometrical optics) represents a light field as a bunch of arrows that point in the direction of propagation. Rays begin at a source and go straight, until an interaction between light and matter causes a change.
The simplifications of ray optics provide a very good way to understand systems of lenses, mirrors, filters, and illumination sources. In many cases, ray optics can elucidate the function of a complicated optical system with just a few lines, triangles, and simple rules. Of course, the simplicity of ray optics comes at a cost. Ray optics glosses over important details like diffraction. Because the fine details are omitted, ray optics alone does not provide insight into detailed performance characteristics of an optical system like resolution. Diffraction and resolution and optical aberrations (which cause simplifying assumptions fail) are discussed on separate pages.
After reading this page and working through the example optical systems, you should be able to use ray optics to understand the function of many optical systems that you encounter or desire to build.
Relationship between light rays and waves
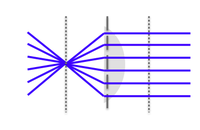
Perhaps the most fundamental solution to Maxwell's equations is the spherical wave, in which light propagates from a point in space uniformly in all directions. It's called a spherical wave because all points at an equal distance from the source — on the surface of a sphere — have the same magnitude electric (and magnetic) field at every point in time. The ray representation of a spherical wave is just a bunch of arrows with their tails on the source and their heads pointing outward, as shown in figure Figure 1. (Most ray diagrams yourepresent a two-dimensional slice of space.) Since the source is isotropic, it's okay draw a ray in pretty much any direction you feel like. In most cases, certain rays are more helpful for understanding a system than others.
Another fundamental solution to Maxwell's equation is the plane wave. In plane waves, the electric field has the same magnitude in all planes perpendicular to the direction of propagation. Conceptually, a plane wave propagating in the z direction is generated by an infinite number of identical, in-phase point sources uniformly distributed in a plane at $ z=-\infty $. Wavefront and ray representations of the plane wave are shown in Figure Figure 2. Plane waves are a useful model for some circumstances, but real plane waves cannot be generated because of their infinite extent (which means a real plane wave would require an infinite amount of power).
Complicated sources such as a luminous object can be modeled as a summation of many point sources.
Interactions between light and matter
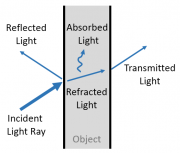
When a ray encounters an object, it may be:
- Reflected
- Refracted (the light is bent by the material properties of the object)
- Absorbed (often turned into thermal energy)
- Transmitted
- Scattered in a random direction
- Or some combination of the above
Reflection and refraction
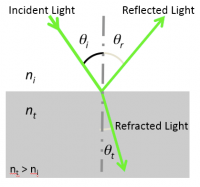
When light reflects, the angle of the reflected ray is equal to the angle of the incident ray: $ \theta_r=\theta_i $. Both angles are measured relative to a vector normal to the surface. Incident and reflected rays are in the same plane.
Light incident at an interface between two media will be partly reflected back into the first medium and partly transmitted to the second medium. The speed of light will be different in the two media based on their material properties. The index of refraction $ n $ for each material is defined as the ratio of the speed of light in vacuum, $ c $, by the speed of light in the medium $ v $. More succinctly, $ n = c / v $. When the light changes speed in the second medium, its direction of propagation also changes. This phenomenon is known as refraction. The transmitted light propagates at an angle described by Snell's law:
- $ n_i\ \sin \theta_i = n_t\ \sin \theta_t $
with θ the angle measured from the normal of the boundary, $ n $ the refractive index of the medium (which has no units), and the subscripts $ i $ and $ t $ referring to the incident and transmitted light, respectively.
Note that Snell's law implies that light passing from a medium of lower index to a higher index of refraction ($ n_t > n_i $) bends toward the surface normal ($ \theta_t < \theta_i $), whereas light traveling from a higher index to a lower index of refraction bends away from the normal. Remember, a higher index means a lower velocity of light in the medium.
An example of using Snell's law: critical angle and total internal reflection
- Snell's law includes the concept of a critical angle $ \theta_c $ for the incident light ray. As the angle of the incident ray approaches $ \theta_c $, the angle $ \theta_t $ approaches 90o. Beyond $ \theta_c $, total internal reflection takes place. In this regime the ray obeys the rules of reflection above.
- Recalling that $ \sin (90^o) = 1 $, one can derive
- $ \theta_c = \sin ^{-1} \left ( {n_t \over n_i} \right ) $
- All fiber optic communication takes advantage of the phenomenon of total internal reflection. The core medium of a fiber is covered by another medium with a lower index of refraction, called the cladding. Thus if light enters the fiber at an angle less than $ \theta_c $, and if the fiber is not bent too far, then the entering light will emerge at the end of the fiber minus only losses in the fiber, plus losses due to other practicalities of the real world of course.
Spherical lenses and image formation
Refraction at a spherical boundary
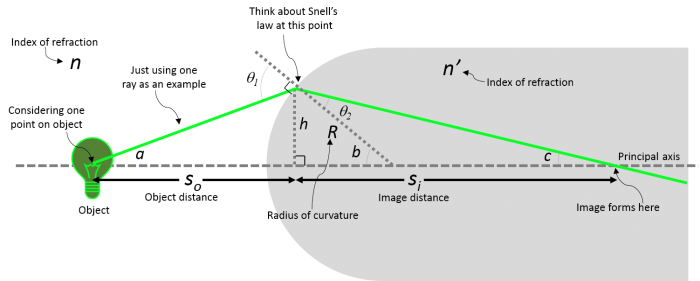
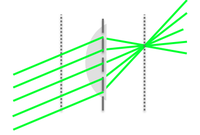
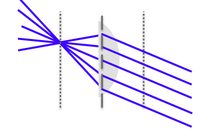
Lenses are one of the most common components of optical instruments. There are many types of lenses, but the most common ones are spherical lenses, which have curved surfaces. To better understand how they manipulate light, let's consider what happens to light at a spherical boundary.
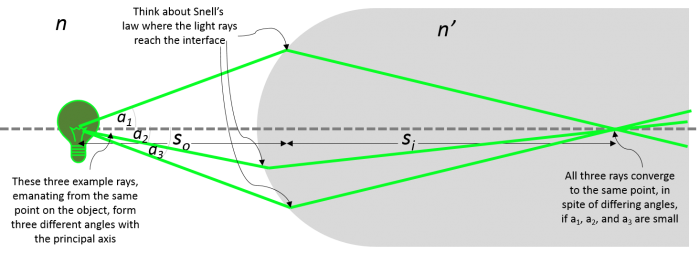
The figure below demonstrates how light rays from a point on an object (the light bulb) can focus to a point after passing through a spherical boundary. The depicted angles and defined lengths can be used to calculate where the light will focus. Even though we only pick a few rays to look at, remember that each point on the object acts as a point source where there are light rays emanating from them in all directions.
Gaussian optics assumptions
As we begin to deal with multiple boundaries, it can become complicated to solve many geometric equations to find where the image will form. In order to make more tractable calculations for us to use when designing our optical systems, we rely on a few first-order, or Gaussian optics, approximations:
- Paraxial (or small-angle) approximation:
- Assumes that light rays make a small angle with the principal axis (a straight line perpendicular to the center of the curved surface, also called the optical axis)
- $ \theta \approx \sin\ \theta \approx \tan\ \theta $
- $ \cos\ \theta \approx 1 $
- (These relations are obtained from the first-order terms of the polynomial expansions of $ \sin \theta = \theta - {\theta^3 \over {3!}} + {\theta^5 \over {5!}} - ... $ and $ \cos \theta = 1 - {\theta^2 \over {2!}} + {\theta^4 \over {4!}} - ... $ and are accurate to 1% if $ \theta < 10^o $.)
- Thin-lens approximation:
- $ R << S_o,\ S_i $
- with $ R $ defined as the radius of curvature of the lens, $ S_o $ as the distance between the lens and the object, and $ S_i $ the distance between the lens and the image.
- These paraxial and thin-lens engineering approximations simplify most optical systems by enabling the use of a short set of ray tracing rules for spherical lenses. These rules reduce many optics problems to more intuitive geometry problems.
- Deviations from these assumptions result in optical aberrations.
- More on thick lenses can be found in the book 'Optics' by Eugene Hecht (Addison-Wesley, 2002, ISBN 0805385665).
Object and image positions
Now, with our Gaussian optics assumptions, we can use Snell's law to predict the image position of an object, formed by a spherical interface (refer to light bulb image above):
- $ n\ \sin \theta_1 = n'\ \sin \theta_2 $
- $ \sin \theta_1 \approx \sin a + \sin b \approx {h \over S_o} + {h \over R} $
- $ \sin \theta_2 \approx \sin b - \sin c \approx {h \over R} - {h \over S_i} $
- $ {n \over S_o} + {n' \over S_i} = {(n'\ - n)\over R} $
Note that equation does not depend on angle a!
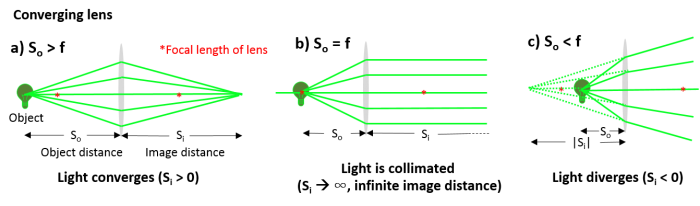
Massaging this equation gives three possible relationships between $ S_i $ and $ S_o $:
- There's no need to memorize these relationships; they just serve to show the different behaviors of light as it passes through the spherical boundary. We will see these behaviors again when we look at lenses having two spherical boundaries in the next section.
| a) Light converges
$ S_o > {n\ R \over (n'\ - n)}\ \Rightarrow S_i > 0 $ , |
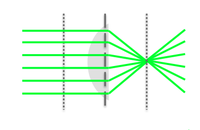
b) Light is collimated
$ S_o = {n\ R \over (n'\ - n)}\ \Rightarrow S_i \to + \infty $, |
c) Light diverges
$ S_o < {n\ R \over (n'\ - n)}\ \Rightarrow S_i < 0 $ |
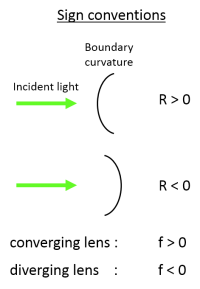
Note the sign convention is that if $ S_i < 0 $, the light diverges, and a virtual image is formed at a distance $ |S_i| $ in front of the lens, on the same side of the lens as the light source (virtual images will be discussed more in a following section).
Lenses
Let's put two spherical interfaces together to make a spherical lens. Each lens consists of two spherical interfaces with radii of curvature $ R_1 $ and $ R_2 $. Its focal length $ f $ is where the image is formed when an object is at infinity.
Types of spherical lenses
A practical note: to minimize spherical aberrations, the general rule is to position the curved side of the lens toward the collimated/straight light.
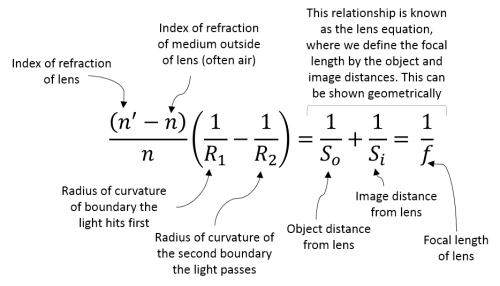
Lens maker's formula
Using the equation we derived earlier to find the image position after light passes through one spherical boundary, we can apply the formula twice--once for each spherical boundary of a simple lens, to calculate where the image will form after light passes through the entire lens. If we maintain our thin lens approximation, and take the image from the first refraction as the object for the second one, we can derive the lens maker's formula:
This formula shows us that the focal length of the lens is a characteristic of the lens, based on its radii of curvature and relevant indices of refraction.
Ray tracing
Based on what we've learned about how light is redirected when passing through lenses, we can come up with a set of rules to simplify our analysis of optical systems. With the technique of ray tracing, we can figure out where images are formed, whether they're upside down, magnified, etc.
Principles
Image formation with a lens
When an object gives off its own light (like a light bulb) or is illuminated, we can imagine that the object is made up of many point sources, where each point on the object is emitting or scattering light in all directions. After refraction, all the rays from a single point in the object plane reach the same location in the image plane, forming an image. The image can be either real or virtual. A real image is one that can be seen if you put a screen on the image plane. A virtual image cannot be seen if a screen is at the image plane since there is no place the rays actually come together; it needs another lens (such as your eye) in order to view it. More examples of real and virtual images are described in a following section.
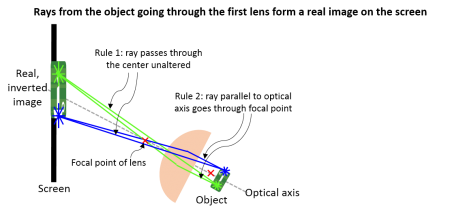
Let's look at a ray tracing example of a single lens producing a real, inverted image:
| Step 1: Pick a ray that you know how to trace (here we pick a point at the top of the object and use Rule 1) |
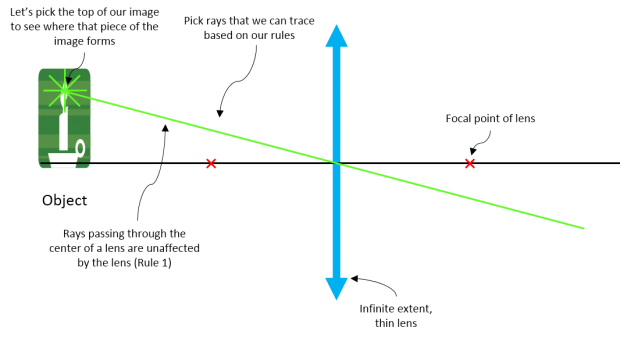
|
| Step 2: Pick more rays emanating from the same point that you can trace based on our rules (here we use Rule 2). See where they converge to form an image |
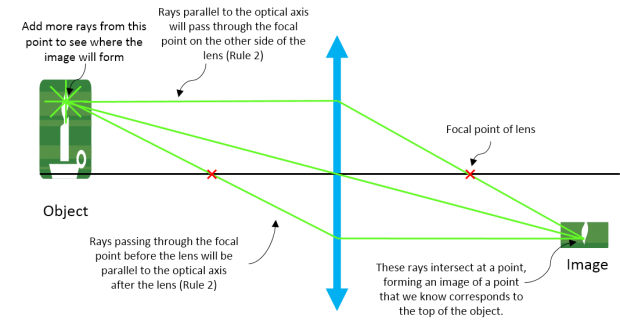
|
| Step 3: Pick rays from a different point on the object (this time we pick a point on the bottom and use Rule 1 again). |
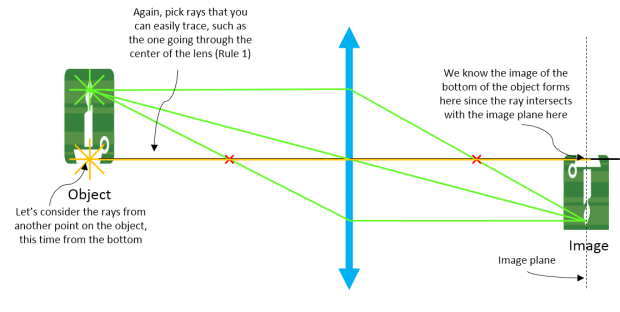
|
| Step 4: For completeness, let's look at more rays emanating from the second point we picked to see where they converge. Here, we use Rule 3. |
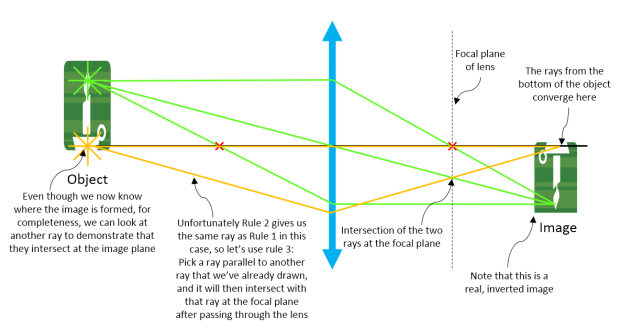
|
Exercise for the reader: Can you use ray tracing to demonstrate the lens equation geometrically? You'll probably need to use similar triangles. Remember, that the lens equation is the relationship between the focal length of the lens, the object distance, and the image distance:$ {1 \over S_o} + {1 \over S_i} = {1\over f} $
Using this relationship, you can see why light going through a converging lens can produce three different results (this is similar to what we saw earlier for light passing through a spherical boundary). Whether the light converges, diverges, or is collimated depends on where the object is relative to the focal length of the lens:
Examples of real and virtual images
Let's use ray tracing to walk through a few examples of real and virtual images. In these examples we will consider the lens of your eye and the image formed on the retina.
| Example 1: Real, inverted image. This is like the ray tracing example shown in the previous section. Don't worry if you can't draw all the rays shown below; there are rays you can draw based on our rules that will show you the same result (you should be able to identify those rays). | |||||||||||||||||||||
| |||||||||||||||||||||
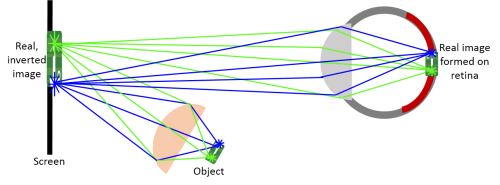
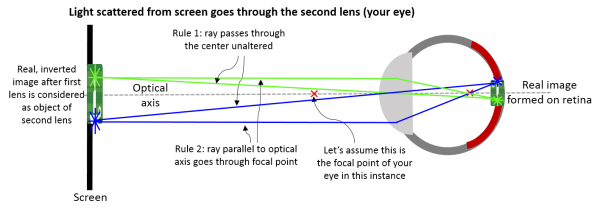
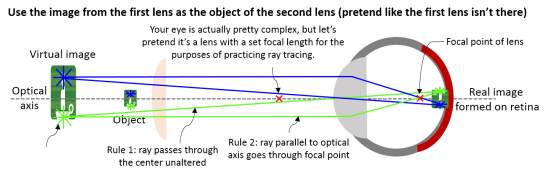
| Example 2: Real image. This time the image is not inverted. This scenario is taking the image of one lens and making it the object of the second lens (your eye). Since the image gets inverted after each lens, it is at the original orientation after passing through the second lens. | |||||||||||||||||||||
| |||||||||||||||||||||
| Example 3: Observing a real image on a screen. | |||||||||||||||||||||
| |||||||||||||||||||||
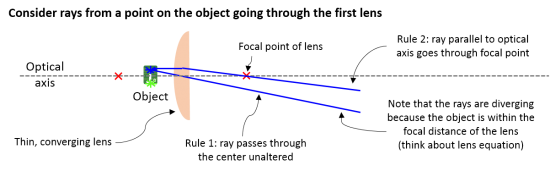
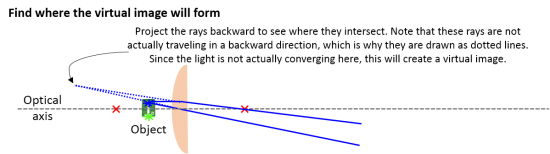
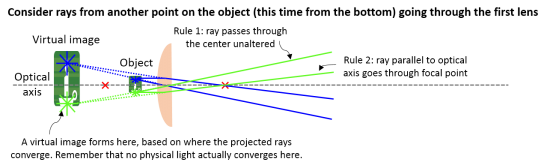
| Example 4: Observing a virtual image. An object placed within the focal distance of a lens produces a virtual image that can be observed through a second lens (like your eye). This is how a magnifying glass works. | |||||||||||||||||||||
| |||||||||||||||||||||
| |||||||||||||||||||||
More ray tracing examples
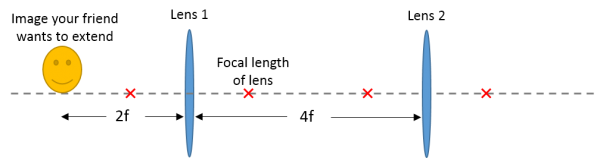
Example 1: Relay lens system
Your friend is building an endoscope, where she wants to faithfully extend an image across a long distance. She proposes a system composed of two convex lenses having the same focal length (f) shown below.
A) Trace the rays to check her work and see where the image is formed.
B) Is the final image the same orientation as the original image, or is it inverted?
C) Use the lens equation to find the distance between the final image and the one she started with.
Once you've worked it out on your own, you can check your work here.
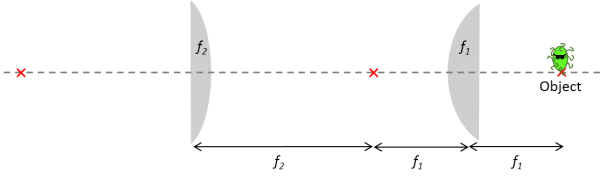
Example 2: Compound microscope
There is a cool bacterium you want to study in closer detail so you want to build a microscope to see it. You are told that you can build a microscope by placing two positive lenses (having focal lengths $ f_1 $ and $ f_2 $) at a separation distance equal to the sum of their focal lengths as shown below.
A) Trace the rays to show how your microscope works and where the image is formed. Is the image real or virtual? upright or inverted? Note that this time the object is on the right and the image will form at the left.
B) Calculate how much magnification you get from this optical system.
C) Will your microscope still work if we change the distance between the lenses?
D) Does changing the distance between the lenses affect the amount of magnification you achieve?
Once you've worked it out on your own, you can check your work here.
Example 3: Beam expanders
Say you're building a microscope and you want to expand the coverage of light that is illuminating your sample. You decide you want to build a beam expander to accomplish this. Assume that the incident light is collimated and you want the resulting light from your beam expander to also be collimated. Come up with two ways to make a beam expander using only two lenses each time--one way with two converging lenses, and another way with one converging and one diverging lens. For each system, answer the following questions:
A) At what distance do the two lenses have to be for the light to still be collimated when exiting the second lens?
B) How much have you magnified the beam after the second lens?
C) Is the final image inverted or upright?
D) What happens if you switch the order of the lenses?
Once you've worked it out on your own, you can check your work here. Solutions are only shown for the method using a diverging and converging lens.