Difference between revisions of "Electronics primer"
(→Solving problems: strategy) |
(→Limits of ideal elements: more realistic model of a battery) |
||
| Line 260: | Line 260: | ||
[[Image:309_epd_battery-model-plot.jpg|thumb|center|400px|Figure 17: '''More realistic battery model: ''i-v'' plot.''']] | [[Image:309_epd_battery-model-plot.jpg|thumb|center|400px|Figure 17: '''More realistic battery model: ''i-v'' plot.''']] | ||
| − | |||
| − | |||
From the model diagram, we see that a real battery only sources a full 9V when no load is applied. As current increases, supplied voltage decreases linearly, with negative slope equalling internal resistance. Here is just one simple example of how we can learn about a system by perturbing it -- whether theoretically or experimentally. In this case we found the function relating voltage and current by imagining putting a load on the battery. Note that the equation we found is ultimately ''not'' dependent on the resistance of this added load <math>R_m</math>. | From the model diagram, we see that a real battery only sources a full 9V when no load is applied. As current increases, supplied voltage decreases linearly, with negative slope equalling internal resistance. Here is just one simple example of how we can learn about a system by perturbing it -- whether theoretically or experimentally. In this case we found the function relating voltage and current by imagining putting a load on the battery. Note that the equation we found is ultimately ''not'' dependent on the resistance of this added load <math>R_m</math>. | ||
Finally, note that the symbol for a real battery is different from that of the ideal voltage source shown earlier. A typical battery symbol looks like Figure 18A; an arbitrary number of additional lines may be shown in some cases (since most batteries actually contain multiple electrochemical cells), as in Figure 18B. | Finally, note that the symbol for a real battery is different from that of the ideal voltage source shown earlier. A typical battery symbol looks like Figure 18A; an arbitrary number of additional lines may be shown in some cases (since most batteries actually contain multiple electrochemical cells), as in Figure 18B. | ||
| + | |||
| + | [[Image:Public-Domain_Battery_symbol.png|thumb|right|500px|Figure 18B: '''Multi-cell battery symbol from public domain.''']] | ||
| + | [[Image:Another-PD-Battery-Symbol.png|thumb|center|50px|Figure 18A: '''Single-cell battery symbol from public domain.''']] | ||
<br style="clear:both;"/> | <br style="clear:both;"/> | ||
Revision as of 01:48, 12 October 2012
Overview: Should I read this thing?
This primer is intended to quickly get electronics newbies comfortable with circuit interpretation by providing clear definitions and systematic mathematical approaches, without unnecessary detail.
If you don’t feel comfortable defining an open or short circuit across arbitrary nodes, aren’t sure how to keep your voltage and current signs consistent, and perhaps even barely remember what series versus parallel means, then this guide is for you. You probably want to read all of it, preferably sections 1-4 before the second lecture on electronics (and section 5 in concert with the first electronics problem set). You’ll get more out of lecture if you’re not struggling with the basics.
If you do feel comfortable with the basic concepts and math in theoretical form, but have no clue how these relate to instruments, breadboards, and what leads are touching where, then you can probably skip this guide and focus your efforts on completing Module 0 instead.
References to the relevant sections of Agarwal and Lang (6.002 textbook, 2005 edition) are included for those seeking to further solidify their understanding.
Motivation: Where is this all leading and why should I care?
Circuit representations are useful for solving problems in many engineering domains -- electrical, mechanical, thermal, hydraulic, etc. Any system of linear ordinary differential equations is amenable to circuit analysis. For simplicity, we’ll start with circuit elements whose behavior is not frequency dependent, namely resistors and sources, and build up to more complex systems involving capacitors and inductors in lecture/lab and perhaps someday a subsequent primer.
Defining essential circuit elements and variables: v, i, R
Primary definitions
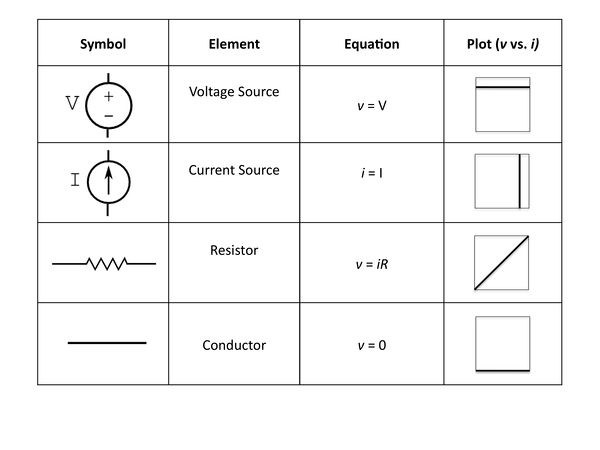
Table 1 lists the name, symbol, constitutive relation and its graphical representation for each of four simple idealized elements: a voltage source, a current source, a resistor, and a conductor. Each constitutive equation and associated plot relate voltage (v) across an element and current (i) through that element.
Current reflects the flow rate of charge carriers such as electrons and by convention is positive in the direction of positive charge flow, which means the electrons are actually flowing in the negative direction. Voltage reflects the electrical potential difference between two points. The higher the voltage, the greater the current flow (always down the potential gradient, because electrons are attracted up the potential gradient) through a given element. To make circuit analysis tenable, each element is treated as having a uniform v and i.[1]
An element is bracketed by terminals, one designated (+) and the other (-). Terminals may be shown as filled or open circles to indicate whether or not that terminal connects to another electrical element. (Open circles represent no connection.) Pairs of terminals are sometimes called ports, whether for a single element or across multiple elements. A port approach is particularly useful for abstracting away (black-boxing) multiple circuit elements and treating them as an equivalent element with defined inputs and/or outputs. We'll return to this idea in sections 5.4 and 5.6.
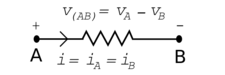
A voltage v and current i can be defined at any terminal. For terminals A and B in Figure 1, the element voltage $ v = v_{AB} = v_A - v_B $ and the element current $ i = i_A = i_B $. Here, $ v_A $ and $ v_B $ are the absolute potentials (defined relative to a reference), and v is the potential difference between the two terminals.
Expanding upon Table 1,
- An ideal voltage source maintains a set potential difference across its terminals no matter what current is being drawn through it. Thus, its voltage versus current graph is simply a horizontal line. A real source such as a battery does not exhibit this behavior. However, such non-ideal elements can be modeled as combinations of ideal linear elements, as described in section 5.6.
- Similarly, an ideal current source provides a set current no matter what potential difference exists across its terminals. Real sources include op-amps.
- Resistance reflects the tendency of an element to draw current and also its tendency to dissipate energy. A linear resistor obeys Ohm’s law, $ v = iR $, at any instant in time. Real resistors are well represented by the model resistor equation only so long as the current and voltage do not exceed their maximum combined ratings.
- Ideal conductors have no resistance, meaning that no potential difference appears across them for any value of current flow through them. No voltage drop in turn results in no energy dissipation. Ideal conductors are a fine model for real wires.
Elements such as sources and resistors are connected at their terminals by wires in order to form circuits. To make circuit analysis tenable, elements are treated as interacting only through their terminals; in other words, electromagnetic fields associated with a given element are internal to it. When this assumption does not hold, more complex elements called capacitors and inductors can be integrated into the circuit.
Two limiting cases of the resistor element are useful for solving circuit problems: the open circuit and the short circuit (Fig. 2). Infinite resistance means that no current passes through that element; this is also called an open circuit across said element and is equivalent to an unconnected port. Zero resistance means no potential difference appears across the element; this is also called a short circuit across that element and is equivalent to an ideal wire.
Illustrative circuit analogies
We are now in a position to appreciate some analogies to electronic circuits. We’ll only describe in detail the most physically intuitive one, while the rest are listed in Table 2.
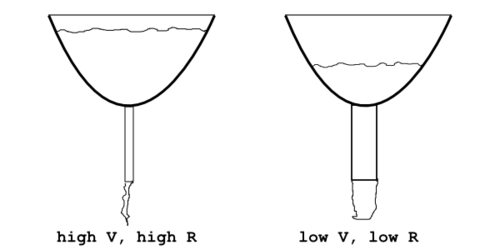
In a hydraulic system (Fig. 3), pressure differences between two points are analogous to voltages in electronic circuits. A water reservoir is like a voltage source, and water flow is analogous to current flow. The higher the pressure differential (greater amount/height of water in the reservoir), the faster the volumetric flow, all else being equal. Resistance can be thought of as the narrowness of the conduit connecting two points. The narrower the pipe, the slower the flow, all else being equal. Or it can be thought of as a pipe packed with beads. The smaller the beads, or the greater in number, the slower the flow, all else being equal.
Essential units
$ v = iR $
[Voltage] = [Amps] [Ohms] = A Ω
Or in a more practical configuration,
[Voltage] = [milliAmps] [kiloOhms] = mA kΩ
Another useful quantity that you will encounter is power, or energy transfer per time. Some circuits may be solved by energy balance alone: for example, energy supplied by a voltage source may be dissipated in resistors or stored in capacitors. Note that power out of an element is negative, and power into an element is positive, by convention.
$ p = vi $
[Watts] = [Volts] [Amps] = V A
= [Joule/Coloumb] [Coulomb/second] = [Joule/second] = J/s = W
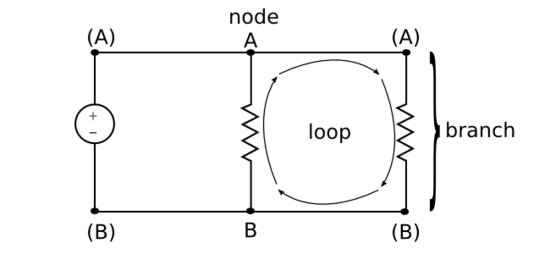
Connecting circuit elements
Multiple elements may be joined at their terminals to build a circuit (Fig. 4). The joined terminals are now called nodes. Any path between two (independent -- see below) nodes is called a branch. Any path from one node back around to itself is called a loop. We’ll revisit these terms when we solve circuit problems in section 5.
Note that two (or more) apparent nodes that are connected by an ideal conductor are considered equivalent, because the conductor by definition cannot maintain a potential difference. Thus, A and the (A)'s above represent only one independent node, not three, as do B and the (B)'s. The two Steve's are of course independent nodes :)
Now is a good time to emphasize the difference between an element variable and a node variable. The element voltage $ v_{AB} $ is the difference between the two node voltages, $ v_A $ and $ v_B $. In other words, an element voltage equals the potential difference across two terminals, while a node voltage equals the absolute potential at a terminal. Of course, this "absolute" potential must still be with respect to a common reference point.
Series and parallel
When two elements are joined end to end, they are said to be in series. In this case, the (-) terminal of one element is joined to the (+) terminal of the second element. If instead the (+) terminals of the two elements are connected, as are their (-) terminals, then the elements are said to be in parallel.
Resistors in series are additive: $ R = R_1 + R_2 $.
Resistors in parallel are inversely additive: $ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} $, and thus $ R = \frac{R_1 R_2}{R_1 + R_2}. $
These relationships are consistent with resistance being proportional to length and inversely proportional to area for a given material. The current that flows through each resistor in series must be identical, while for resistors in parallel, the voltage across each one must be identical. We will learn why when we discuss Kirchoff’s laws in section 5.1.
Similarly, voltage sources connected in series are additive, with current unaffected. Voltage sources linked in parallel maintain the potential difference of a single voltage source (so all sources must be identical or things get tricky ), with increased current flow.[2]
Series and parallel relationships can be used to reduce complex circuits to more simple ones as an intermediate step in problem-solving.
Ground
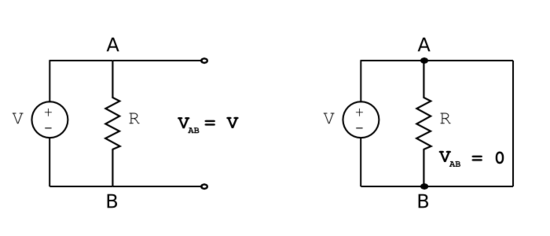
Note that a voltage, or potential difference, is always a relative description. For example, for a voltage source the nominal (supposed) voltage -- say, 12 V -- is the potential difference between the (+) and (-) terminals. It is usually really convenient when solving circuit problems to define the (-) terminal as zero. (The relative nature of voltage allows this arbitrary choice.) This potential level is called ground. Ground can be considered a reservoir of electrons. By definition, any terminal connected to ground by a wire must also be at 0V. Ground is also the usual reference point for defining terminal/node voltages.
However, there is nothing stopping us from defining the (+) and (-) terminals as +6V and -6V, and this may be convenient in certain problems.
Understanding equivalent diagram topologies and notations, part 1
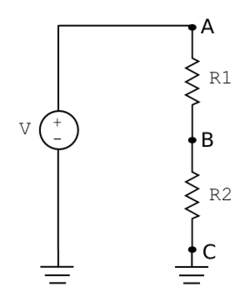
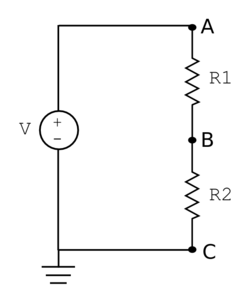
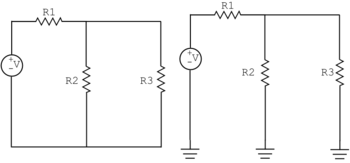
A common group of elements comprises a voltage source and two resistors in series. For reasons we shall see shortly, this grouping or "primitive" is called a voltage divider. Two common ways to depict this circuit are shown below.
We can see that the voltage at node C is trivially 0, and that at node A is the maximum source voltage, because these are connected to the voltage source by ideal wires. The voltage at node B depends on the relative values of the two resistors.
As an example, let's take V = 12 V, $ R_1 $ = 200 Ω, and $ R_2 $ = 600 Ω. Each resistor is described by $ v=iR $, where i must be uniform in this purely series-connected circuit. Ohm's law also applies to the circuit as a whole when using the overall series equivalent resistance $ R_{eq} $, namely the sum of the two resistances. Thus, $ v = 12 \text{V} = i R_{eq} = i (R_1 + R_2) = i (200 + 600)\Omega $, which can be solved for i = 15 mA.
The first resistor is described by $ v_{AB}= i R_1 =15 mA * 200 \Omega $. Thus, it has an element voltage of $ v_{AB} = 3 \text{V} $, and the node joining the two resistors has node voltage $ v_B = 12 - 3 = 9 \text{V} $. Indeed, solving the second resistor equation $ v_{BC}= i R_2 =15 \text{mA} * 600 \Omega $ yields 9 V (with $ v_C $= 0 , of course).
Clearly, a voltage divider "divides" the voltage drop across resistors in series in proportion to their resistances. In sections 5.2-5.3 we will see a more universally applicable way to solve this problem, when we cannot rely on our intuition as much. Then we will imagine connecting measurement devices to the circuit and also further discuss topology.
Some other examples of topogically equivalent circuits are shown below (Fig 8).
Putting it all together: solving circuit problems
Solving problems: fundamentals/theory
Two key relationships provide the foundation for circuit analysis: Kirchoff’s circuit law and Kirchoff’s voltage law, hereafter KCL and KVL. KCL is based on charge conservation: at any node, the sum of the current magnitudes flowing in must equal the sum of the current magnitudes flowing out. When solving problems in which current directions are trivially known, this form of the law works well.
And now we see why current must be equal for elements connected in series: at the shared node, current coming out from the first element must have the same magnitude as current coming into the second element. No other branches exist at that node.
Returning to the issue of signs, current always flows from the (+) to the (-) terminal for an element, that is, from higher to lower voltage (except in a voltage source). However, the terminal definitions may not always be obvious/known in advance of solving the circuit problem. To keep signs straight, it will be convenient to have a systematic relationship between i and v signs. This relationship is described in the problem-solving section just below.
KVL is based on conservation of energy: the sum of the element voltages (potential difference across each element) around a loop is zero. Equivalently, the potential difference between the starting and ending node in a loop (that is, the same node) must be zero.
Take, for example, the three node voltage divider from section 4.3. Applying KVL directly in a clockwise direction, $ v_{AB} + v_{BC} +v_{CA} = 3+ 9 -12 =0. $ KVL is even more straightforwardly applied using node voltages. Again going clockwise, clearly node voltages $ v_A - v_B + v_B - v_C - v_A + v_C = 0 $, without even plugging in numbers.
Now we also see why voltage must be equal for elements connected in parallel: the two shared nodes form a loop, and hence the potential differences across the two elements must be identical.
Solving problems: strategy
One rigorous way to solve circuit problems is to write the constitutive relation for each element (B equations for B branches), every independent KCL statement (N-1 equations for N nodes), and every independent KVL statement (B-1+N equations for B branches). Then algbraic substitutions are made until every element voltage and current is known. Often it is not obvious which substitutions will most quickly yield the quantities that are actually of interest in that problem.
A faster universal approach for solving circuit problems indirectly incorporates KVL and requires fewer KCL statements. Rarely can there be confusion about which choice of equations will quickly yield meaningful results. (For very complex circuits, however, linear rather than simple algebraic approaches may be required.)
Recall that while an element voltage is the potential difference across said element, a node voltage is the potential difference between that node and a common reference point – usually ground. (If these definitions doesn't sound familiar, see Figure 1 under Primary definitions and also review Connecting circuit elements.)
Working with node voltages rather than element voltages makes KVL implicit, as we saw in the voltage divider example above. The basic approach is then to write a single KCL equation per unknown node voltage, while immediately substituting in the element constitutive laws in terms of voltages and resistances.[3]
Now we make our alternative statement of KCL: the sum of all currents flowing into a node is zero, where current now includes both magnitude and sign. For $ i=v/R $ relationships, always subtract the close node voltage from the far node voltage — $ V_{far} - V_{close} $ — to calculate the element voltage v in the numerator, and the sign of the calculated current should always come out right[4]. It will be positive if flowing in as assumed, and negative if actually flowing out. Using this sign convention, a current pointing toward the node is positive, and one pointing away fom the node is negative. However, a voltage source whose far node is the negative terminal must yield a positive current, because a source does work to push charge against the usual direction. [Last part maybe could be phrased more clearly]
Understanding equivalent diagram topologies and notations, part 2
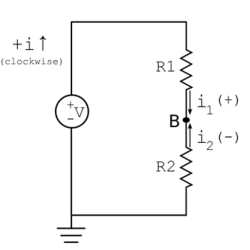
Let’s return to the two-resistor voltage divider described in section 4.3 above to practice our systematic approach for solving circuits, calling the single non-trivial node of interest B for consistency. We can apply KCL to calculate it:
$ i_1 + i_2 = 0 = \frac{12-v_B}{200} + \frac{0-v_B}{600} \to \text{nominal}\ v_B = 9 \text{V}. $
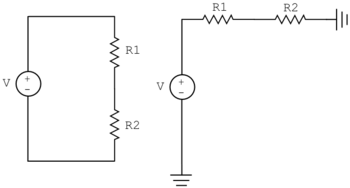
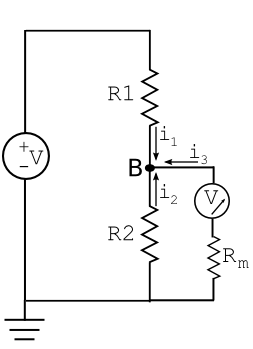
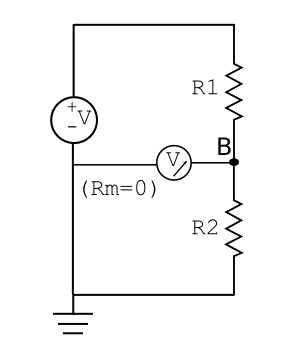
Now let’s imagine connecting a voltmeter to measure the voltage at node B. To read the correct relative potential, the voltmeter must also be connected at ground. In other words, the second resistor and the voltmeter with associated resistance $ R_m $ are in parallel. Before attaching the voltmeter, the access port of interest can be shown as:
After attaching the voltmeter, three equivalent circuit diagrams depicting the system are:
The voltmeter must have a high enough resistance that it does not draw current and substantially affect $ v_B $. If instead it has a comparable resistance, say 300 Ω, let’s calculate the effect on $ v_B $ using our usual KCL approach:
$ i_1 + i_2 + i_3 = 0 = \frac{12-v_B}{200} + \frac{0-v_B}{600} +\frac{0-v_B}{300} \to \text{nominal}\ v_B = 6 V. $
This value is unacceptably far off from our nominal 9 V. However, if $ R_m $ is increased an order of magnitude, to 3 kΩ, $ v_B $is a respectable 8.57 V. (Try it!)
Wouldn't it be nice to calculate $ v_B $ for a given $ R_m $ without repeating the full calculation each time? The next section describes just such a method.
Thevenin equivalent circuits
Topological equivalence between circuits implies that wires have been moved around or added in place of shorthand. There is also such a thing as functional equivalence between circuits. In fact, any complex circuit consisting only of voltage sources and resistors can be reduced to a circuit with only a single voltage source and resistor! This equivalent circuit cannot be empirically distinguished from the multi-component one.
Let’s return to the voltage divider example with a port across the second resistor. We want to know how the circuit as a whole responds at this access port when there is no load on it, i.e., no element in which energy can be dissipated. We calculate the equivalent circuit by three steps.
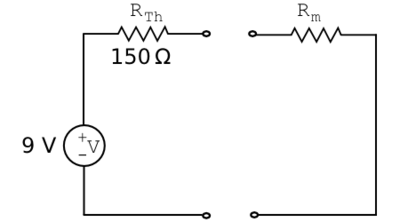
First we calculate the open circuit voltage ($ V_{oc} $) at that port, namely 9 V as above in section 5.3.
Next we calculate the short circuit current. In this hypothetical, the attached voltmeter has no internal resistance and behaves as a wire (Fig 12). In turn, $ v_B $ is shorted to ground, and current magnitude is dependent only on $ R_1 $, not both $ R_1 $ and $ R_2 $. Hence, the short circuit current $ I_{sc} = 12 \text{V}/200 \Omega = 0.06 \text{A} = 60 \text{mA} $.
Finally, the Thevenin resistance $ R_{Th} = \frac{V_{oc}}{I_{sc}} = \frac{9 \text{V}}{0.06 \text{A}} = 150 \Omega $. The Thevenin equivalent circuit is shown in Figure 13.
Now how does this two-component circuit reduction help us? The voltmeter (or any element!) can be connected in series with $ R_{Th} $, and $ v_B $ calculated immediately by the simple voltage divider relation, $ \frac{V R_m}{R_{tot}}. $
An alternative and direct calculation of $ R_{Th} $ is the total resistance at the port as viewed looking into the circuit (with voltage sources changed to wires): here, $ R_1 $ and $ R_2 $ in parallel.
Alternative problem-solving strategies
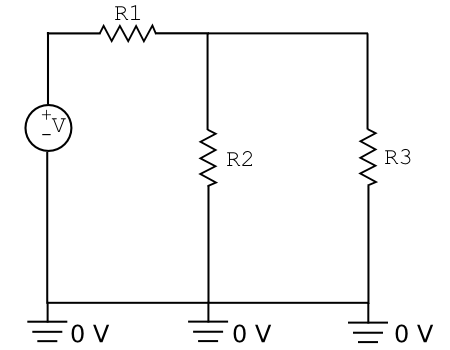
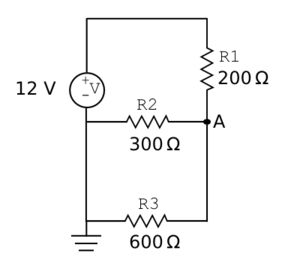
Circuit problems can be approached in many ways[5] and in the interests of time we will primarily treat the approach that (nearly) universally works, namely the node voltage/KCL method described above. Let’s briefly look at one example of another approach.
Consider the circuit shown at right. The parallel resistors $ R_2 $ and $ R_3 $ can be temporarily collapsed into an equivalent single resistor. Its resistance is given by
$ R_{parallel} = \frac{R_2 R_3}{R_2 + R_3} = 200 \Omega. $
Then, the current through the purely series-connected circuit is simply
$ i = \frac{V}{R_{tot}} = \frac{V}{R_1 + R_{parallel}} $
where $ R_{tot} = 400 \Omega $ and by the voltage divider relation $ v_A $ is clearly 6 V. That is, half the voltage drop occurs across each 200 Ω resistor, the physically real one and the imaginary one (equivalent to two real ones).
We next expand the circuit to once more include the real, parallel branches. The potential difference across each branch must be the same $ v_A $, and thus the individual currents can be calculated from $ v_A =i_{branch x}R_{branch x} $.
For example, $ i_2 =\frac{v_A}{R_2} = \frac{6}{300} = 20 \text{mA} $.
As expected, $ i_2 $ and $ i_3 $ sum to the current through the first resistor.
Yet another general circuit-solving approach is applying energy conservation equations.
Limits of ideal elements: more realistic model of a battery
Recall the ideal i-v curves for our four elements, referring to Table 1 under Primary definitions .
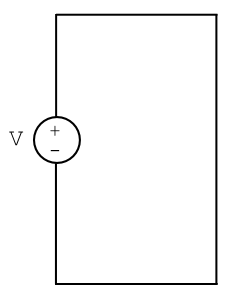
Let’s model a battery as an ideal voltage source connected to no other elements except ideal wires (Fig. 14).
What is the current flowing through this circuit? The resistance of the wires is zero, implying that the current is infinite! Therefore this model, and the associated horizontal i-v curve, is not realistic.
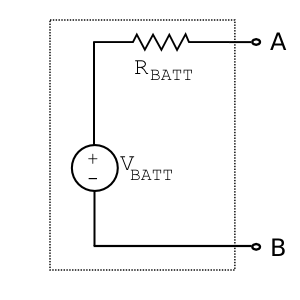
Instead, let’s model the battery as having an internal resistance, $ R_{BATT} $ (Fig. 15). To investigate the i-v curve, we’ll view the output port formed by nodes A and B.
When the port is not connected to anything, resistance is infinite and current is zero. There is no load on the battery, and thus the output voltage at node A must be the full $ V_{BATT} $. This useful quantity is our by now familiar open circuit voltage, $ V_{oc} $.
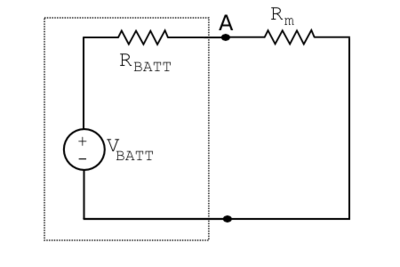
Next, let’s attach a voltmeter to the port with an associated resistance $ R_m $.
When we assume that $ R_m = 0 $, $ v_A $ is shorted to ground. Thus, the current i is at its maximum, namely the short circuit current:
$ I_{sc} = \frac{V_{BATT}}{R_{BATT}} $.
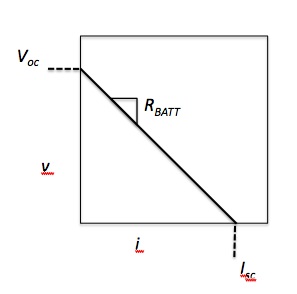
These two quantities define two points on our new, more realistic, i-v curve! Presumably a line connects them, but let’s prove it by solving this simple circuit. We’ll practice our systematic approach once again.
The only unknown node voltage is $ v_A $. The other nodes are either ground or $ V_{BATT} $ by definition of a perfect conductor. Hence we want to solve KCL at $ V_{BATT} $, substituting in the relevant $ v=iR $ constitutive relations:
$ i1 + i2 = 0 = \frac{9-v_A}{R_{BATT}} + \frac{0-v_A}{R_m} = 0 $
and substituting for $ R_m $ using $ I = \frac{v_A}{R_m} $
to simplify to $ v_A = 9-I * R_{BATT} $,
indeed the equation of a line.
From the model diagram, we see that a real battery only sources a full 9V when no load is applied. As current increases, supplied voltage decreases linearly, with negative slope equalling internal resistance. Here is just one simple example of how we can learn about a system by perturbing it -- whether theoretically or experimentally. In this case we found the function relating voltage and current by imagining putting a load on the battery. Note that the equation we found is ultimately not dependent on the resistance of this added load $ R_m $.
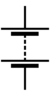
Finally, note that the symbol for a real battery is different from that of the ideal voltage source shown earlier. A typical battery symbol looks like Figure 18A; an arbitrary number of additional lines may be shown in some cases (since most batteries actually contain multiple electrochemical cells), as in Figure 18B.
Thanks for reading! I'll appreciate any constructive feedback about the utility of this guide. Agi Stachowiak 21:11, 11 October 2012 (EDT)
References
- ↑ For more about circuit assumptions and abstraction layers, see Agarwal 1.1-1.4: The power of abstraction, The lumped circuit abstraction, The lumped matter discipline, and Limitations of the lumped circuit abstraction.
- ↑ See Agarwal 1.5.1, Practical two-terminal elements: Batteries, for more information.
- ↑ Slightly more complex approaches must be taken for cases in which a voltage source has a negative terminal that is not connected to ground. See Agarwal 3.3.2, The node method: Floating independent voltage sources.
- ↑ You could alternatively subtract the far node from the close node; the key is to be consistent. May as well memorize what Steve does though!
- ↑ Overall, see chapters 2 (Resistive Networks) and 3 (Network Theorems) of Agarwal. Section 2.4 (Intuitive method of circuit analysis: series and parallel simplification) treats series/parallel reductions, section 3.5 (Superposition) treats superposition, etc.