Difference between revisions of "Electronics primer"
(→Solving problems: strategy) |
MAXINE JONAS (Talk | contribs) (→Thevenin equivalent circuits) |
||
| (215 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
[[Category:20.309]] | [[Category:20.309]] | ||
[[Category:Electronics]] | [[Category:Electronics]] | ||
| + | {{Template:20.309}} | ||
| + | [[Image:xkcd_circuit_diagram.png|thumb|275 px|right|Circuit diagram according to [http://xkcd.com/730/ xkcd].]] | ||
| − | ==Overview | + | ==Overview== |
| − | + | [[Image:309_epd_resistor-fully-labeled.png|thumb|right|Resistor symbol.]] | |
| + | The physical quantities that characterize many types of systems are defined at all points in space and time. In the case of electric circuits, the quantities of interest are charge, electric field, and magnetic field. Maxwell's equations describe the relationship between the three quantities as a function of space and time. Using Maxwell's equations to compute the field and charge at every point is a very thorough approach to analyzing electrical systems. However, such a detailed model includes far too much information to be useful for understanding or designing most circuits made from standard electronic components like resistors and capacitors. Analysis can be dramatically simplified by using a ''lumped element'' circuit model. Lumped element models characterize a system only at a small number of well-defined points by collapsing regions of space into ideal lumped elements. Regions of space that do not significantly impact system behavior are ignored. | ||
| − | + | Lumped electronic elements are idealized abstractions of physical components like resistors and capacitors. A lumped element circuit model represents a system as a network of elements connected together by wires. Each element has two ''state variables'': current and voltage. (The lumped element model for electronic components assumes that magnetic interaction between elements are negligible.) It is possible to create lumped element models of many other types of systems described by two state variables, including thermal, acoustic, hydraulic, and mechanical systems. | |
| − | + | Elements are bounded by terminals. In elements with two terminals, one is typically designated plus (+) and the other minus (-). Every two-terminal element has a single voltage across it and a single current flow through it. The relationship between current through the element and the voltage difference across the element's terminals is defined by a constitutive equation<ref name="CircuitAssumptions"> For more about circuit assumptions and abstraction layers, see Agarwal 1.1-1.4: ''The power of abstraction'', ''The lumped circuit abstraction'', ''The lumped matter discipline'', and ''Limitations of the lumped circuit abstraction''.</ref>. | |
| − | + | Each type of element has an associated graphic symbol. The symbol for a resistor is shown at right. The constitutive equation for an ideal resistor is given by Ohm's law, ''v''=''iR''. | |
| − | == | + | ==Review of electrical units and equations== |
| − | + | ===Voltage=== | |
| − | + | [[Image:309_epd_grouds-example.png|thumb|right|250px|Multi-component circuit with ground nodes emphasized.]] | |
| − | + | Voltage quantifies the electrical potential difference between two terminals. Higher voltages attract electrons more intensely and thus result in larger current flows. Voltage is usually represented by the variable ''v''. | |
| − | + | Electric potential difference has the units of energy divided by charge and is measured in volts, abbreviated with a capital V. Energy is measured in joules (J) and electric charge is measured in coulombs (C)<ref>One mole of electrons has a charge of about 96,500 coulombs.</ref>. 1 V = 1 J/C = 1 kg m<sup>2</sup> / s<sup>2</sup> C. | |
| − | + | Voltage is always measured relative to a reference point. It is useful to designate a particular node as the zero point, called the ''ground node''. You may designate any node at all as ground; however, some choices are more convenient than others. In a circuit with a single voltage or current source, the best choice is usually the negative terminal of the source. The voltage across an element in a network can be found by subtracting the node voltage at its minus terminal from the node voltage at its plus terminal. | |
| − | + | Another possible choice of reference points is ''earth ground''. Earth ground is the potential at which we spend most of our days — the potential of a conductor driven a few feet into the soil. If you are at earth ground potential, the doorknob doesn't shock you when you go to open the door. The ground node in most circuits is usually at a potential close to earth ground, but not always. The third conductor on electrical plugs is connected to earth ground. Since we spend most of our time near earth ground potential, connecting the outer case of electrical equipment to earth ground helps prevent shocks. Earth ground and the circuit ground node may or may not be connected together. | |
| − | + | ||
| − | + | ===Current=== | |
| − | + | Current measures the flow rate of charge through an element. The SI unit for current is amperes, abbreviated amps of just A. 1 A = 1 C/s. A positive current flows from the plus terminal to the minus. The variable ''i'' is usually used to represent current. | |
| − | + | Skip the following paragraph if you want to keep things simple. | |
| − | + | ||
| − | + | The conventional definition of current is the flow rate of positive charge carriers from the plus terminal to the minus terminal. In most of the components you will work with, such as wires, capacitors, and resistors, the charge carriers are negatively charged electrons. Electrons flowing from the minus to the plus terminal create a current with a positive sign. Current in semiconductors is carried by both positive and negative carriers. This is confusing. It's all Benjamin Franklin's fault<ref>http://www.physicsclassroom.com/class/circuits/u9l2c.cfm</ref>. The best approach is not to think about it at all when you are solving circuit problems. Stick to the convention that positive current flows from plus to minus. It doesn't matter for most circuits what the sign of the charge carriers is. If you are doing a gel electrophoresis, on the other hand, the sign of the charge carriers is crucial. | |
| − | + | ===Resistance=== | |
| − | + | Resistance has units of ohms, sometimes abbreviated with the greek letter Ω. 1 Ω = 1 V/A. Resistance is usually denoted by the letter R. | |
| − | + | ||
| − | + | ||
| − | + | ===Power=== | |
| + | Electric power is equal to voltage multiplied by current, ''P'' = ''v i''. Power has units of energy per time called watts, abbreviated with a capital W. 1 W = 1V x 1A = 1 J / s. | ||
| − | + | ==Ideal lumped circuit elements== | |
| − | [[Image: | + | [[Image:309_epd_Table1.jpg|325px|thumb|right|Table of ideal elements.]] |
| + | The table on the right summarizes the characteristics of four ideal elements: a voltage source, a current source, a resistor, and a conductor. The i-v curve in the fourth column shows the constitutive equation graphically, with voltage plotted on the vertical axis and current on the horizontal axis. | ||
| − | = | + | An ideal voltage source maintains a constant potential difference across its terminals regardless of the amount of current flowing through it. Thus, its voltage versus current i-v graph is a horizontal line. The current flowing through an ideal current source is constant no matter what potential difference is across its terminals. The plot is a vertical line. Ideal resistors obey Ohm’s law, ''v'' = ''iR'', which is a sloped line on the voltage versus current graph. Ideal conductors have zero resistance. All points on a conductor have the same voltage. |
| − | + | You can watch a video on ideal circuit elements [https://www.khanacademy.org/science/electrical-engineering/ee-circuit-analysis-topic/circuit-elements/v/ideal-circuit-elements here]. | |
| − | [[Image: | + | ===Connecting circuit elements=== |
| + | [[Image:309_epd_node-loop-terminology.png|thumb|250px|right|Circuit illustrating nodes, branches, and loops.]] | ||
| − | + | Networks of elements are formed by connecting terminals together with wires. A schematic diagram like the one shown at right is one way to specify the connections. Elements interact only through their terminals. Terminals joined together by wires are called nodes. All of the terminals connected to a node have the same voltage, which is unsurprising because they are connected by an an element that by definition has the same potential everywhere. Any path between two independent nodes is called a branch. Any path from one node back around to itself is called a loop. | |
| − | + | Terminals may be shown as filled or open circles to indicate whether or not that terminal connects to another element. Open circles represent no connection. Pairs of terminals are sometimes called ''ports''. A port may encompass a single element or multiple elements. Dividing a circuit into groups of elements that interact through their ports can be a useful way to conceptualize and analyze systems. | |
| − | + | ||
| − | == | + | ==Common circuit patterns== |
| + | Two patterns of connected elements come up so frequently that it is worth memorizing them: series and parallel. Many circuit problems can be simplified by recognizing elements within the system that are connected in series or parallel. | ||
| − | + | ===Series and parallel connections=== | |
| − | + | [[Image:309_epd_series-parallel.png|thumb|250px|right|Resistors in series and parallel.]] | |
| − | + | ||
| − | [ | + | |
| − | + | When two elements are joined end to end, they are said to be in series. In this case, the minus terminal of one element is joined to the plus terminal of the second element. The current flowing through each element connected in series connection is identical. The equivalent resistance of two resistors in series is the sum of the resistances: ''R'' = ''R<sub>1</sub>'' + ''R<sub>2''</sub>. Voltage sources connected in series are added. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | In a parallel connection, the plus terminals of two elements are connected together, as are the minus terminals. The voltage across each of the elements in a parallel connection is the same. The equivalent resistance of two resistors in parallel is: ''R'' = <sup>''R<small>1</small>R<small>2</small>''</sup>/<sub>''R<small>1</small>'' + ''R<small>2</small>''</sub>. | |
| + | <!-->Voltage sources linked in parallel maintain the potential difference of a single voltage source (so all sources must be identical or things get tricky ), with increased current flow.<ref name="SeriesParallelBatteries">See Agarwal 1.5.1, ''Practical two-terminal elements: Batteries'', for more information.</ref> | ||
| + | <--> | ||
| − | + | ===Voltage divider=== | |
| + | [[Image:309_epd_basis-voltage-divider.png|150px|thumb|right]] | ||
| − | + | A very common circuit construct consists of two resistors in series, as shown in the schematic diagram on the right. This type of circuit is called a voltage divider. In a series connection, the same current ''i'' flows through both resistors. The constitutive relation for a resistor is: ''v''=''i''R. Using this equation, the voltage across resistor R<sub>1</sub> is ''i''R<sub>1</sub> and the voltage across R<sub>2</sub> is ''i''R<sub>2</sub>. The minus terminal of R<sub>2</sub> is connected to ground, so the voltage ''V<sub>C</sub>'' at node C is by definition 0 volts. The voltage across R<sub>2</sub> is ''i''R<sub>2</sub>, so the voltage ''V<sub>B</sub>'' at node B is 0+''i''R<sub>2</sub>=''i''R<sub>2</sub>. The ideal source constrains the voltage ''V<sub>A</sub>'' at node A to be V, which must also be equal to the sum of the voltages across the resistors: V = ''i''R<sub>1</sub>+''i''R<sub>2</sub>=''i''(R<sub>1</sub>+R<sub>2</sub>). Substituting for ''V<sub>B</sub>'' into this expression gives an equation for ''V<sub>B</sub>'' in terms of the source voltage V and the resistor values: ''V<sub>B''=V<sup>R<small>2</small></sup>/<sub>R<small>1</small>+R<small>2</small></sub>. If you don't know why the circuit is called a voltage divider, take another look at the equation. | |
| − | + | You can watch a video on voltage dividers [https://www.khanacademy.org/science/electrical-engineering/ee-circuit-analysis-topic/ee-resistor-circuits/v/ee-voltage-divider here]. | |
| − | + | ==Solving circuit problems== | |
| − | === | + | ===Charge and energy conservation=== |
| + | Charge and energy are conserved in electric circuits. Two equations ensure that both quantities are conserved: Kirchoff’s Current Law (KCL) and Kirchoff’s Voltage Law (KVL). | ||
| − | + | The current law states that the sum of the currents flowing into any node must equal zero. In other words, the sum of currents flowing in must equal the sum of the currents flowing out. Applying KCL to the node in-between two resistors in series demonstrates why the current is equal in both. At the shared node, current flowing out of the first element has nowhere else to go. No other branches exist at that node. | |
| − | + | KVL ensures that energy is conserved. The law states that the sum of the potential difference across elements in a loop is zero. In other words, if you go around a loop, you end up at the same point. | |
| − | + | KVL and KCL also offer another rationale for why the potential must be equal across elements connected in parallel. The two shared nodes form a loop. In order to sum to 0, the potential differences across the two elements must be identical. | |
| − | + | ===Node-voltage analysis method=== | |
| + | One rigorous way to solve circuit problems is to write the constitutive relation for each element (B equations for B branches), every independent KCL statement (N-1 equations for N nodes), and every independent KVL statement (B-1+N equations for B branches and N nodes). Then algebraic substitutions are made until every element voltage and current is known. Often it is not obvious which substitutions will most quickly yield the quantities that are actually of interest in that problem. | ||
| − | + | [[Image:309_epd_voltage-divider-w-currents.png|thumb|right|250px|Voltage divider with current flow convention shown. Current flow in this circuit is clockwise. Hence, <math>i_2</math> is negative.]] | |
| + | The node-voltage analysis method is a faster universal approach for solving circuit problems. It indirectly incorporates KVL and requires fewer KCL statements. Rarely can there be confusion about which choice of equations will quickly yield meaningful results. (For very complex circuits, linear rather than simple algebraic approaches may be required.) | ||
| − | + | Recall that while an element voltage is the potential difference across said element, a node voltage is the potential difference between that node and a common reference point – usually ground. (If these definitions don't sound familiar, see Figure 1 under [http://measure.mit.edu/~20.309/wiki/index.php?title=Electronics_Primer#Primary_definitions Primary definitions] and also review [http://measure.mit.edu/~20.309/wiki/index.php?title=Electronics_Primer#Connecting_circuit_elements Connecting circuit elements].) | |
| − | + | Working with node voltages rather than element voltages makes KVL implicit, as we saw in the voltage divider example above. The basic approach is then to write a single KCL equation per unknown node voltage, while immediately substituting in the element constitutive laws in terms of voltages and resistances.<ref name="FloatingSources"> Slightly more complex approaches must be taken for cases in which a voltage source has a negative terminal that is not connected to ground. See Agarwal 3.3.2, ''The node method: Floating independent voltage source''s.</ref> | |
| − | + | To avoid mistakes when using KCL, it is helpful to adopt a consistent way of writing the node equations. One convenient way to do this is to write an expression of the current flowing ''into'' the node through each connected component, sum the expressions, and set the whole thing equal to zero. The expression for the current flowing through an element into the node is obtained by subtracting the voltage at the node under consideration from the voltage at the far end of the element (i.e. the terminal not connected to the node) and dividing by R. All you have to remember is, "the sum of the currents flowing into the node is zero." | |
| − | + | ===Example: measuring voltage=== | |
| + | [[Image:309_epd_voltmeter-voltage-divider.png|thumb|right|250px|Voltage divider with voltmeter attached.]] | ||
| + | Imagine connecting a voltmeter to measure the output of a voltage divider. In order to read the correct potential, the voltmeter must also be connected to ground. A model for the voltmeter includes an ideal meter and a resistance, R<sub>m</sub>. R<sub>m</sub> models the current ''i<sub>3</sub>'' drawn by the voltmeter as it makes its measurement. | ||
| − | + | Before the meter is connected, KCL states that ''i<sub>1</sub>'' + ''i<sub>2</sub>'' = 0. Assuming R<sub>1</sub>=200Ω R<sub>2</sub>=600Ω, and V = 12 V, solving for the voltage at node B gives: | |
| − | + | <br /> | |
| + | <math>\frac{12-v_B}{200} + \frac{0-v_B}{600} \to v_B = 9 \text{V}.</math> | ||
| − | + | <br /> | |
| + | After the voltmeter is connected, R<sub>2</sub> and R<sub>m</sub> are in parallel. The KCL equation becomes: ''i<sub>1</sub>'' + ''i<sub>2</sub>'' + ''i<sub>3</sub>'' = 0. If the voltmeter has a resistance of 300Ω, the voltage at node B is now: | ||
| − | + | <br /> | |
| + | <math>\frac{12-v_B}{200} + \frac{0-v_B}{600} +\frac{0-v_B}{300} \to v_B = 6 V.</math> | ||
| − | + | <br /> | |
| − | + | With R<sub>m</sub>=300Ω, the measured value is far from nominal value of 9V before the meter was connected. To make an accurate measurement, the voltmeter must have a resistance much larger than the resistors in the divider. if R<sub>m</sub> is increased an order of magnitude to 3 kΩ, <math>v_B</math>will be 8.57 V. Now you can see why voltmeters typically have an equivalent resistance of around 10<sup>9</sup> Ω. | |
| − | <br | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
===Thevenin equivalent circuits=== | ===Thevenin equivalent circuits=== | ||
| Line 185: | Line 124: | ||
Let’s return to the voltage divider example with a port across the second resistor. We want to know how the circuit as a whole responds at this access port when there is no load on it, i.e., no element in which energy can be dissipated. We calculate the equivalent circuit by three steps. | Let’s return to the voltage divider example with a port across the second resistor. We want to know how the circuit as a whole responds at this access port when there is no load on it, i.e., no element in which energy can be dissipated. We calculate the equivalent circuit by three steps. | ||
| − | First we calculate the open circuit voltage (<math>V_{oc}</math>) at that port, namely 9 V as | + | First we calculate the open circuit voltage (<math>V_{oc}</math>) at that port, namely 9 V as [http://measure.mit.edu/~20.309/wiki/index.php?title=Electronics_Primer#Example:_measuring_voltage above]. |
| − | Next we calculate the short circuit current. In this hypothetical, the attached voltmeter has no internal resistance and behaves as a wire (Fig 12). In turn, <math>v_B</math> is shorted to ground, and current magnitude is dependent only on <math>R_1</math>, not both <math>R_1</math> and <math>R_2</math>. Hence, the short circuit current <math>I_{sc} = 12 \text{V}/200 \Omega = 0.06 \text{A} = 60 \text{mA} </math>. | + | Next we calculate the short circuit current. In this hypothetical situation, the attached voltmeter has no internal resistance and behaves as a wire (Fig 12). In turn, <math>v_B</math> is shorted to ground, and current magnitude is dependent only on <math>R_1</math>, not both <math>R_1</math> and <math>R_2</math>. Hence, the short circuit current <math>I_{sc} = 12 \text{V}/200 \Omega = 0.06 \text{A} = 60 \text{mA} </math>. |
Finally, the Thevenin resistance <math>R_{Th} = \frac{V_{oc}}{I_{sc}} = \frac{9 \text{V}}{0.06 \text{A}} = 150 \Omega</math>. The Thevenin equivalent circuit is shown in Figure 13. | Finally, the Thevenin resistance <math>R_{Th} = \frac{V_{oc}}{I_{sc}} = \frac{9 \text{V}}{0.06 \text{A}} = 150 \Omega</math>. The Thevenin equivalent circuit is shown in Figure 13. | ||
| Line 195: | Line 134: | ||
An alternative and direct calculation of <math>R_{Th}</math> is the total resistance at the port as viewed looking into the circuit (with voltage sources changed to wires): here, <math>R_1</math> and <math>R_2</math> in parallel. | An alternative and direct calculation of <math>R_{Th}</math> is the total resistance at the port as viewed looking into the circuit (with voltage sources changed to wires): here, <math>R_1</math> and <math>R_2</math> in parallel. | ||
| − | [[Image:309_epd_short-circuit-voltage-divider.png|thumb|left|300px|'''Figure 12: Short circuit current for voltage divider. | + | [[Image:309_epd_short-circuit-voltage-divider.png|thumb|left|300px|'''Figure 12:''' Short circuit current for voltage divider.]] |
[[Image:309_epd_Thevenin-equivalent.png|thumb|center|400px|'''Figure 13: Thevenin reduction of voltage divider.''' The Thevenin equivalent of the previously described voltage divider is shown (left) with an open port ready to be connected to a voltmeter with arbitrary resistance (right).]] | [[Image:309_epd_Thevenin-equivalent.png|thumb|center|400px|'''Figure 13: Thevenin reduction of voltage divider.''' The Thevenin equivalent of the previously described voltage divider is shown (left) with an open port ready to be connected to a voltmeter with arbitrary resistance (right).]] | ||
| Line 202: | Line 141: | ||
===Alternative problem-solving strategies === | ===Alternative problem-solving strategies === | ||
| − | Circuit problems can be approached in many ways<ref name="AlternativeProblemApproaches">Overall, see chapters 2 (''Resistive Networks'') and 3 (''Network Theorems'') of Agarwal. Section 2.4 (''Intuitive method of circuit analysis: series and parallel simplification'') treats series/parallel reductions, section 3.5 (''Superposition'') treats superposition, etc.</ref> and in the | + | Circuit problems can be approached in many ways<ref name="AlternativeProblemApproaches">Overall, see chapters 2 (''Resistive Networks'') and 3 (''Network Theorems'') of Agarwal. Section 2.4 (''Intuitive method of circuit analysis: series and parallel simplification'') treats series/parallel reductions, section 3.5 (''Superposition'') treats superposition, etc.</ref> and in the interest of time we will primarily treat the approach that (nearly) universally works, namely the node-voltage analysis method described above. Let’s briefly look at one example of another approach that can be used on its own or can simplify a complex topology before employing the node-voltage method. |
[[Image:309_epd_three-R-circuit.png|thumb|right|300px|'''Three resistor circuit.''']] | [[Image:309_epd_three-R-circuit.png|thumb|right|300px|'''Three resistor circuit.''']] | ||
| Line 223: | Line 162: | ||
Yet another general circuit-solving approach is applying energy conservation equations. | Yet another general circuit-solving approach is applying energy conservation equations. | ||
| − | == | + | ==Notes on schematic diagrams== |
| − | + | [[Image:309_epd_shorthand-voltage-divider.png|150px|thumb|right]] | |
| − | + | Another way to draw a schematic of a voltage divider circuit is shown on the right. Instead of connecting all the ground nodes together with lines, ground nodes are indicated by a ground symbol. Complex circuits have many connections to the ground node. Drawing all of the ground connections can make the schematic diagram hard to follow. This diagram represents exactly the same system as the one in which a line connected node C to the minus terminal of the voltage source. | |
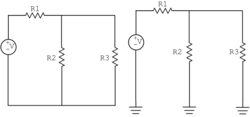
| − | + | Some other examples of topogically equivalent circuits are shown below. | |
| − | [[Image: | + | {| |
| − | [[Image: | + | |[[Image:309_epd_topological-equivalence-3R.png|250px|left|thumb|Equivalent schematic diagrams of resistors in parallel.]] |
| − | + | |[[Image:309_epd_topological-equivalence-2R.png|250px|right|thumb|Equivalent schematic diagrams of resistors in series.]] | |
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==References== | ==References== | ||
<references /> | <references /> | ||
| − | |||
{{Template:20.309 bottom}} | {{Template:20.309 bottom}} | ||
Latest revision as of 13:50, 19 October 2018
Overview
The physical quantities that characterize many types of systems are defined at all points in space and time. In the case of electric circuits, the quantities of interest are charge, electric field, and magnetic field. Maxwell's equations describe the relationship between the three quantities as a function of space and time. Using Maxwell's equations to compute the field and charge at every point is a very thorough approach to analyzing electrical systems. However, such a detailed model includes far too much information to be useful for understanding or designing most circuits made from standard electronic components like resistors and capacitors. Analysis can be dramatically simplified by using a lumped element circuit model. Lumped element models characterize a system only at a small number of well-defined points by collapsing regions of space into ideal lumped elements. Regions of space that do not significantly impact system behavior are ignored.
Lumped electronic elements are idealized abstractions of physical components like resistors and capacitors. A lumped element circuit model represents a system as a network of elements connected together by wires. Each element has two state variables: current and voltage. (The lumped element model for electronic components assumes that magnetic interaction between elements are negligible.) It is possible to create lumped element models of many other types of systems described by two state variables, including thermal, acoustic, hydraulic, and mechanical systems.
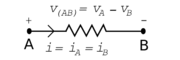
Elements are bounded by terminals. In elements with two terminals, one is typically designated plus (+) and the other minus (-). Every two-terminal element has a single voltage across it and a single current flow through it. The relationship between current through the element and the voltage difference across the element's terminals is defined by a constitutive equation[1].
Each type of element has an associated graphic symbol. The symbol for a resistor is shown at right. The constitutive equation for an ideal resistor is given by Ohm's law, v=iR.
Review of electrical units and equations
Voltage
Voltage quantifies the electrical potential difference between two terminals. Higher voltages attract electrons more intensely and thus result in larger current flows. Voltage is usually represented by the variable v.
Electric potential difference has the units of energy divided by charge and is measured in volts, abbreviated with a capital V. Energy is measured in joules (J) and electric charge is measured in coulombs (C)[2]. 1 V = 1 J/C = 1 kg m2 / s2 C.
Voltage is always measured relative to a reference point. It is useful to designate a particular node as the zero point, called the ground node. You may designate any node at all as ground; however, some choices are more convenient than others. In a circuit with a single voltage or current source, the best choice is usually the negative terminal of the source. The voltage across an element in a network can be found by subtracting the node voltage at its minus terminal from the node voltage at its plus terminal.
Another possible choice of reference points is earth ground. Earth ground is the potential at which we spend most of our days — the potential of a conductor driven a few feet into the soil. If you are at earth ground potential, the doorknob doesn't shock you when you go to open the door. The ground node in most circuits is usually at a potential close to earth ground, but not always. The third conductor on electrical plugs is connected to earth ground. Since we spend most of our time near earth ground potential, connecting the outer case of electrical equipment to earth ground helps prevent shocks. Earth ground and the circuit ground node may or may not be connected together.
Current
Current measures the flow rate of charge through an element. The SI unit for current is amperes, abbreviated amps of just A. 1 A = 1 C/s. A positive current flows from the plus terminal to the minus. The variable i is usually used to represent current.
Skip the following paragraph if you want to keep things simple.
The conventional definition of current is the flow rate of positive charge carriers from the plus terminal to the minus terminal. In most of the components you will work with, such as wires, capacitors, and resistors, the charge carriers are negatively charged electrons. Electrons flowing from the minus to the plus terminal create a current with a positive sign. Current in semiconductors is carried by both positive and negative carriers. This is confusing. It's all Benjamin Franklin's fault[3]. The best approach is not to think about it at all when you are solving circuit problems. Stick to the convention that positive current flows from plus to minus. It doesn't matter for most circuits what the sign of the charge carriers is. If you are doing a gel electrophoresis, on the other hand, the sign of the charge carriers is crucial.
Resistance
Resistance has units of ohms, sometimes abbreviated with the greek letter Ω. 1 Ω = 1 V/A. Resistance is usually denoted by the letter R.
Power
Electric power is equal to voltage multiplied by current, P = v i. Power has units of energy per time called watts, abbreviated with a capital W. 1 W = 1V x 1A = 1 J / s.
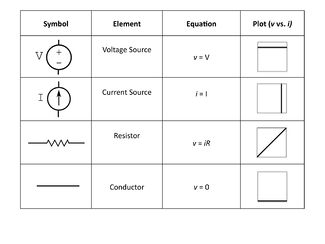
Ideal lumped circuit elements
The table on the right summarizes the characteristics of four ideal elements: a voltage source, a current source, a resistor, and a conductor. The i-v curve in the fourth column shows the constitutive equation graphically, with voltage plotted on the vertical axis and current on the horizontal axis.
An ideal voltage source maintains a constant potential difference across its terminals regardless of the amount of current flowing through it. Thus, its voltage versus current i-v graph is a horizontal line. The current flowing through an ideal current source is constant no matter what potential difference is across its terminals. The plot is a vertical line. Ideal resistors obey Ohm’s law, v = iR, which is a sloped line on the voltage versus current graph. Ideal conductors have zero resistance. All points on a conductor have the same voltage.
You can watch a video on ideal circuit elements here.
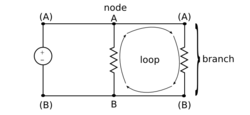
Connecting circuit elements
Networks of elements are formed by connecting terminals together with wires. A schematic diagram like the one shown at right is one way to specify the connections. Elements interact only through their terminals. Terminals joined together by wires are called nodes. All of the terminals connected to a node have the same voltage, which is unsurprising because they are connected by an an element that by definition has the same potential everywhere. Any path between two independent nodes is called a branch. Any path from one node back around to itself is called a loop.
Terminals may be shown as filled or open circles to indicate whether or not that terminal connects to another element. Open circles represent no connection. Pairs of terminals are sometimes called ports. A port may encompass a single element or multiple elements. Dividing a circuit into groups of elements that interact through their ports can be a useful way to conceptualize and analyze systems.
Common circuit patterns
Two patterns of connected elements come up so frequently that it is worth memorizing them: series and parallel. Many circuit problems can be simplified by recognizing elements within the system that are connected in series or parallel.
Series and parallel connections
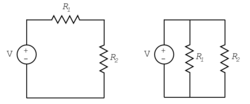
When two elements are joined end to end, they are said to be in series. In this case, the minus terminal of one element is joined to the plus terminal of the second element. The current flowing through each element connected in series connection is identical. The equivalent resistance of two resistors in series is the sum of the resistances: R = R1 + R2. Voltage sources connected in series are added.
In a parallel connection, the plus terminals of two elements are connected together, as are the minus terminals. The voltage across each of the elements in a parallel connection is the same. The equivalent resistance of two resistors in parallel is: R = R1R2/R1 + R2.
Voltage divider
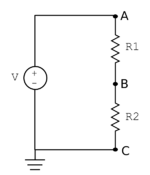
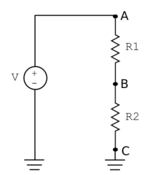
A very common circuit construct consists of two resistors in series, as shown in the schematic diagram on the right. This type of circuit is called a voltage divider. In a series connection, the same current i flows through both resistors. The constitutive relation for a resistor is: v=iR. Using this equation, the voltage across resistor R1 is iR1 and the voltage across R2 is iR2. The minus terminal of R2 is connected to ground, so the voltage VC at node C is by definition 0 volts. The voltage across R2 is iR2, so the voltage VB at node B is 0+iR2=iR2. The ideal source constrains the voltage VA at node A to be V, which must also be equal to the sum of the voltages across the resistors: V = iR1+iR2=i(R1+R2). Substituting for VB into this expression gives an equation for VB in terms of the source voltage V and the resistor values: VB=VR2/R1+R2. If you don't know why the circuit is called a voltage divider, take another look at the equation.
You can watch a video on voltage dividers here.
Solving circuit problems
Charge and energy conservation
Charge and energy are conserved in electric circuits. Two equations ensure that both quantities are conserved: Kirchoff’s Current Law (KCL) and Kirchoff’s Voltage Law (KVL).
The current law states that the sum of the currents flowing into any node must equal zero. In other words, the sum of currents flowing in must equal the sum of the currents flowing out. Applying KCL to the node in-between two resistors in series demonstrates why the current is equal in both. At the shared node, current flowing out of the first element has nowhere else to go. No other branches exist at that node.
KVL ensures that energy is conserved. The law states that the sum of the potential difference across elements in a loop is zero. In other words, if you go around a loop, you end up at the same point.
KVL and KCL also offer another rationale for why the potential must be equal across elements connected in parallel. The two shared nodes form a loop. In order to sum to 0, the potential differences across the two elements must be identical.
Node-voltage analysis method
One rigorous way to solve circuit problems is to write the constitutive relation for each element (B equations for B branches), every independent KCL statement (N-1 equations for N nodes), and every independent KVL statement (B-1+N equations for B branches and N nodes). Then algebraic substitutions are made until every element voltage and current is known. Often it is not obvious which substitutions will most quickly yield the quantities that are actually of interest in that problem.
The node-voltage analysis method is a faster universal approach for solving circuit problems. It indirectly incorporates KVL and requires fewer KCL statements. Rarely can there be confusion about which choice of equations will quickly yield meaningful results. (For very complex circuits, linear rather than simple algebraic approaches may be required.)
Recall that while an element voltage is the potential difference across said element, a node voltage is the potential difference between that node and a common reference point – usually ground. (If these definitions don't sound familiar, see Figure 1 under Primary definitions and also review Connecting circuit elements.)
Working with node voltages rather than element voltages makes KVL implicit, as we saw in the voltage divider example above. The basic approach is then to write a single KCL equation per unknown node voltage, while immediately substituting in the element constitutive laws in terms of voltages and resistances.[4]
To avoid mistakes when using KCL, it is helpful to adopt a consistent way of writing the node equations. One convenient way to do this is to write an expression of the current flowing into the node through each connected component, sum the expressions, and set the whole thing equal to zero. The expression for the current flowing through an element into the node is obtained by subtracting the voltage at the node under consideration from the voltage at the far end of the element (i.e. the terminal not connected to the node) and dividing by R. All you have to remember is, "the sum of the currents flowing into the node is zero."
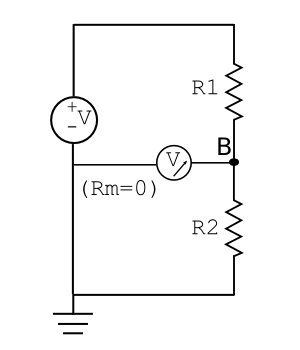
Example: measuring voltage
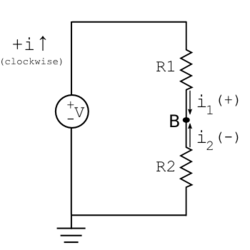
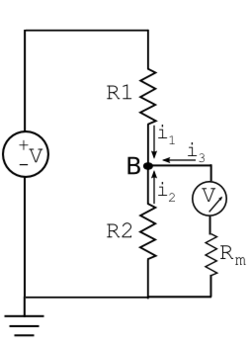
Imagine connecting a voltmeter to measure the output of a voltage divider. In order to read the correct potential, the voltmeter must also be connected to ground. A model for the voltmeter includes an ideal meter and a resistance, Rm. Rm models the current i3 drawn by the voltmeter as it makes its measurement.
Before the meter is connected, KCL states that i1 + i2 = 0. Assuming R1=200Ω R2=600Ω, and V = 12 V, solving for the voltage at node B gives:
$ \frac{12-v_B}{200} + \frac{0-v_B}{600} \to v_B = 9 \text{V}. $
After the voltmeter is connected, R2 and Rm are in parallel. The KCL equation becomes: i1 + i2 + i3 = 0. If the voltmeter has a resistance of 300Ω, the voltage at node B is now:
$ \frac{12-v_B}{200} + \frac{0-v_B}{600} +\frac{0-v_B}{300} \to v_B = 6 V. $
With Rm=300Ω, the measured value is far from nominal value of 9V before the meter was connected. To make an accurate measurement, the voltmeter must have a resistance much larger than the resistors in the divider. if Rm is increased an order of magnitude to 3 kΩ, $ v_B $will be 8.57 V. Now you can see why voltmeters typically have an equivalent resistance of around 109 Ω.
Thevenin equivalent circuits
Topological equivalence between circuits implies that wires have been moved around or added in place of shorthand. There is also such a thing as functional equivalence between circuits. In fact, any complex circuit consisting only of voltage sources and resistors can be reduced to a circuit with only a single voltage source and resistor! This equivalent circuit cannot be empirically distinguished from the multi-component one.
Let’s return to the voltage divider example with a port across the second resistor. We want to know how the circuit as a whole responds at this access port when there is no load on it, i.e., no element in which energy can be dissipated. We calculate the equivalent circuit by three steps.
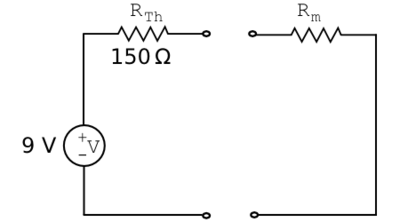
First we calculate the open circuit voltage ($ V_{oc} $) at that port, namely 9 V as above.
Next we calculate the short circuit current. In this hypothetical situation, the attached voltmeter has no internal resistance and behaves as a wire (Fig 12). In turn, $ v_B $ is shorted to ground, and current magnitude is dependent only on $ R_1 $, not both $ R_1 $ and $ R_2 $. Hence, the short circuit current $ I_{sc} = 12 \text{V}/200 \Omega = 0.06 \text{A} = 60 \text{mA} $.
Finally, the Thevenin resistance $ R_{Th} = \frac{V_{oc}}{I_{sc}} = \frac{9 \text{V}}{0.06 \text{A}} = 150 \Omega $. The Thevenin equivalent circuit is shown in Figure 13.
Now how does this two-component circuit reduction help us? The voltmeter (or any element!) can be connected in series with $ R_{Th} $, and $ v_B $ calculated immediately by the simple voltage divider relation, $ \frac{V R_m}{R_{tot}}. $
An alternative and direct calculation of $ R_{Th} $ is the total resistance at the port as viewed looking into the circuit (with voltage sources changed to wires): here, $ R_1 $ and $ R_2 $ in parallel.
Alternative problem-solving strategies
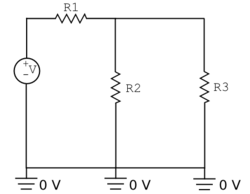
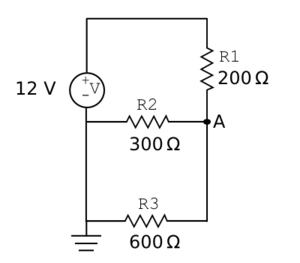
Circuit problems can be approached in many ways[5] and in the interest of time we will primarily treat the approach that (nearly) universally works, namely the node-voltage analysis method described above. Let’s briefly look at one example of another approach that can be used on its own or can simplify a complex topology before employing the node-voltage method.
Consider the circuit shown at right. The parallel resistors $ R_2 $ and $ R_3 $ can be temporarily collapsed into an equivalent single resistor. Its resistance is given by
$ R_{parallel} = \frac{R_2 R_3}{R_2 + R_3} = 200 \Omega. $
Then, the current through the purely series-connected circuit is simply
$ i = \frac{V}{R_{tot}} = \frac{V}{R_1 + R_{parallel}} $
where $ R_{tot} = 400 \Omega $ and by the voltage divider relation $ v_A $ is clearly 6 V. That is, half the voltage drop occurs across each 200 Ω resistor, the physically real one and the imaginary one (equivalent to two real ones).
We next expand the circuit to once more include the real, parallel branches. The potential difference across each branch must be the same $ v_A $, and thus the individual currents can be calculated from $ v_A =i_{branch x}R_{branch x} $.
For example, $ i_2 =\frac{v_A}{R_2} = \frac{6}{300} = 20 \text{mA} $.
As expected, $ i_2 $ and $ i_3 $ sum to the current through the first resistor.
Yet another general circuit-solving approach is applying energy conservation equations.
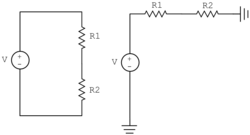
Notes on schematic diagrams
Another way to draw a schematic of a voltage divider circuit is shown on the right. Instead of connecting all the ground nodes together with lines, ground nodes are indicated by a ground symbol. Complex circuits have many connections to the ground node. Drawing all of the ground connections can make the schematic diagram hard to follow. This diagram represents exactly the same system as the one in which a line connected node C to the minus terminal of the voltage source.
Some other examples of topogically equivalent circuits are shown below.
References
- ↑ For more about circuit assumptions and abstraction layers, see Agarwal 1.1-1.4: The power of abstraction, The lumped circuit abstraction, The lumped matter discipline, and Limitations of the lumped circuit abstraction.
- ↑ One mole of electrons has a charge of about 96,500 coulombs.
- ↑ http://www.physicsclassroom.com/class/circuits/u9l2c.cfm
- ↑ Slightly more complex approaches must be taken for cases in which a voltage source has a negative terminal that is not connected to ground. See Agarwal 3.3.2, The node method: Floating independent voltage sources.
- ↑ Overall, see chapters 2 (Resistive Networks) and 3 (Network Theorems) of Agarwal. Section 2.4 (Intuitive method of circuit analysis: series and parallel simplification) treats series/parallel reductions, section 3.5 (Superposition) treats superposition, etc.
</div>