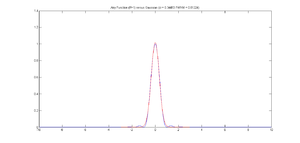
Converting Gaussian fit to Rayleigh resolution
One method for measuring resolution is to fit a Gaussian function to an image of a very small source such as a fluorescent PSF microsphere. If the source is small enough, the image approximates the optical system's point spread function. As evidenced by the plot at right, the Gaussian function looks a lot like the central maximum of the Airy function.
The Rayleigh resolution of the Airy function shown is 1. The σ of the corresponding Gaussian is 0.34493. Thus, to convert the Gaussian fit to Rayleigh resolution, multiply σ by 1/0.34493 = 2.8991.
Note that some Gaussian fitting functions (such as gaussfit) return sqrt(2) * σ, instead of σ. In this case, multiply the value returned by 1/(sqrt(2) * 0.46869) = 1.50869. This occurs because the gaussfit function does not include the customary factor of two in its denominator. The equation implemented by gaussfit is:
F = (a(1) * exp(-((X - a(5)) .^ 2 / (a(2) ^ 2) + (Y-a(6)) .^ 2 / (a(3) ^ 2))) + a(4));
Here is the code that generated the plot:
xAxis = -10:0.01:10; % generate an Airy disk profile with a normalized resolution R=1 firstBesselZero = 3.8317; airyFunction = (2 * besselj( 1, firstBesselZero * xAxis)./ (firstBesselZero * xAxis) ).^2; airyFunction(xAxis == 0) = 1; % use nonlinear regression to fit a Gaussian function to the Airy disk gaussianFunction = @(parameters, xdata) parameters(2) * exp( -xdata .^ 2 / (2 * parameters(1) .^ 2) ); bestFitGaussianParameters = nlinfit(xAxis, airyFunction, gaussianFunction, [1 1]); lsqcurvefit(gaussianFunction, [1 1], xAxis, airyFunction); bestFitGaussian = gaussianFunction(bestFitGaussianParameters, xAxis); sigma = bestFitGaussianParameters(1); sigmaToFwhmConversionFactor = 2 * sqrt(2*log(2)); fwhm = sigmaToFwhmConversionFactor * sigma; % plot the results plot(xAxis, airyFunction); hold on; plot(xAxis, bestFitGaussian, 'r'); title(texlabel(['Airy Function (R=1) versus Gaussian (sigma = ' num2str(sigma) ' FWHM = ' num2str(fwhm) ')']));