Difference between revisions of "Complex Number Review"
From Course Wiki
(→Finding the phase) |
|||
| Line 20: | Line 20: | ||
=Finding the phase= | =Finding the phase= | ||
| − | + | [[Image: Phase.png|thumb|center|200px]] | |
{{Template:20.309 bottom}} | {{Template:20.309 bottom}} | ||
Revision as of 17:31, 11 August 2016
Overview
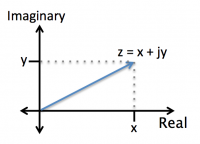
Complex numbers include a real component and an imaginary component, which includes the imaginary number $ j = \sqrt{-1} $. We can represent a complex number like this: $ z = x + jy $, where $ x $ is the real part and $ y $ is the imaginary part. Complex numbers can be represented on a plot as shown on the right, where the horizontal axis corresponds to the real part and the vertical axis corresponds to the imaginary part.Since we are often dealing with sinusoidal waveforms, it can be helpful to think of complex numbers also in exponential form. According to Euler's identities,
- $ e^{j \theta} = cos(\theta) + j sin(\theta) $
- $ cos(\theta) = {e^{j\theta} + e^{-j\theta}\over 2} $
- $ sin(\theta) = {e^{j\theta} - e^{-j\theta}\over 2} $
Finding the magnitude
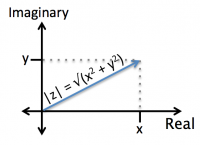
In the rectangular form of the complex number $ z = x + jy $, we can see that the magnitude of $ z $ (the length of the arrow in the below plot) is:
- $ |z| = \sqrt{x^2 + y^2} $
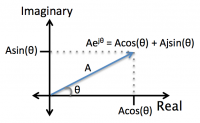
In exponential form, we can see that the magnitude of $ Ae^{j \theta} $ is:
- $ |Ae^{j \theta}| = A $
Thus, when two complex numbers are multiplied, their magnitudes multiply. Similarly, when two complex numbers are divided (as we often see in transfer functions), their magnitudes are divided. For example, $ |{Ae^{j \theta} \over Be^{j \theta}}| = {A \over B} $