20.309: Biological Instrumentation and Measurement

Introduction
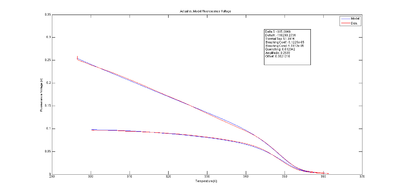
Measured photodiode voltage,
Vf,measured plotted versus block temperature,
θblock along with model photodiode voltage,
Vf,model.
In Assignment 8, you made some improvements to your DNA melting instrument, and (hopefully) collected some spectacular data. This assignment will focus on extracting useful information from the data in order to make some quantitative conclusions.
The fluorescence voltage, Vf,measured(t), that you measured in lab depends not only on the parameters of interest, ΔH°, and ΔS°, but also on:
- the double stranded DNA concentration Cds(t) (which we know from the outset)
- the dynamics of the temperature cycling system
- thermal quenching of the fluorophore
- photobleaching
- responsivity and offset of the instrument
- binding kinetics of the dye
The goal for Assignment 9 is to write a model for Vf,measured that takes these effects into account and use nonlinear regression to estimate the parameters of this function. The model proposed here adheres to Dr. George E. P. Box's excellent advice on modeling, in that it is both wrong and useful. Some of the assumptions are more dubious than others. You might ask: "why don't we just fit the DNA melting curve to a higher order polynomial?" - great question. We are developing a mechanistic model, which means that we hope the fit parameters will give us some insight into the physical processes behind the DNA melting system. Fitting an arbitrary function may be useful to interpolate the data, but provides no physical insights.
Onward!
Assignment details
In this assignment you will write the code to analyze your DNA melting data in three parts:
- In Part 1, you will define the functions for each phenomenon and combine them into a single fit function;
- In Part 2, you will create some simulated data to verify your code and test your model.
- In Part 3, you will use the code on your real data and think about the statistical model you'll use to identify your unknown sample.
| Warning: you will need the code written in this assignment to analyze your data in Assignment 10. Drop at your own risk!!
|

|
Turn in all of your work (comprehensive list below) on Stellar in a single PDF file named <lastname><firstname>Assignment9.pdf.
Part 1:
- Turn in your code for SimulateLowPass, SimulatePhotobleaching, SimulateThermalQuenching and Vmodel (once it has been tested!)
Part 2:
- Plot the following items on the same set of axes. Don't forget to include a legend!
- your simulated fluorescence data as a function of block temperature
- your model function with initial best-guess parameters as a function of block temperature
- your model function with fitted par meters (obtained by nlinfit) as a function of block temperature
- Calculate the uncertainty for each parameter from the fit, and fill in the uncertainty table, making sure to include appropriate units and significant figures.
- Plot the normalized uncertainty for each fit parameter as a function of the noise magnitude. Which parameter appears to be the most sensitive to noise? the least?
- Using the expressions we derived in class for dsDNA concentration at a given temperature, derive an expression for the melting temperature, $ T_m $in terms of $ \Delta H $ and $ \Delta S $. The melting temperature is defined as the temperature for which the fraction of double stranded DNA equals 0.5. Calculate the melting temperature for each noise level from 0.01 to 0.05.
Part 3:
- Plot your fluorescence data as a function of block temperature, your model function with initial guesses, and your model function with best fit parameters on the same set of axes.
- Record your estimates for ΔH and ΔS. Calculate Tm.
- How do these thermodynamic parameters compare to the predicted values you obtained from DINAmelt or OligoCalc?
- For one fit result, plot the residuals vs.
- time,
- temperature, and
- fluorescence.
- Write a function to convert fluorescence into fraction of double stranded DNA. For at least one experimental trial, plot $ \text{DnaFraction}_{inverse-model} $ versus the sample temperature $ T_{sample} $ (example plot). On the same set of axes plot DnaFraction versus $ T_{sample} $ using the best-fit values of ΔH and ΔS. Finally, plot simulated dsDNA fraction vs. temperature using data from DINAmelt or another melting curve simulator.
- Explain the statistical method you will use to identify your group's unknown sample in Assignment 10.
- State the acceptance/rejection criteria for any hypotheses tests you will use.
- This page may be a helpful reference: Identifying the unknown DNA sample.
Finally,
- Append all of the code (not yet included) that you wrote for Parts 1, 2 and 3 of this assignment.
|
Navigation
Back to
20.309 Main Page

