Difference between revisions of "Nonlinear regression"
| Line 1: | Line 1: | ||
{{Template:20.309}} | {{Template:20.309}} | ||
| + | <blockquote> | ||
| + | <div> | ||
| + | ''… the safe use of regression requires a good deal of thought and a good dose of skepticism'' | ||
| + | |||
| + | — [http://mitsloan.mit.edu/faculty/detail.php?in_spseqno=41132 Arnold Barnett] | ||
| + | </div> | ||
| + | </blockquote> | ||
| + | |||
| + | |||
| + | ==Review of linear regression== | ||
| + | |||
| + | Linear Regression is a method for finding the magnitude of the relationship between two variables that co-vary. The technique assumes that a straight line characterizes the relationship between the two quantities: 𝑦=𝛽𝑥+𝛼, where 𝛽 is the true slope and 𝛼 is the true intercept. If two points on the line, (<i>x<sub>i</sub></i>, <i>y<sub>i</sub></i>); <i>i</i> = {1,2}, are precisely known, solving for the exact values of 𝛼 and 𝛽 is trivial. Unfortunately, all physical measurements include noise. The presence of noise precludes finding the exact values of 𝛼 and 𝛽. | ||
| + | |||
| + | The function of linear regression is to produce estimates of 𝛼 and 𝛽, denoted by <i>α̂</i> and <i>β̂</i>, from a sample of N value pairs (<i>x<sub>i</sub></i>, <i>y<sub>i</sub></i>); <i>i</i> = {1, ..., N} that includes noise in the <i>y</i>-values. Thus, the samples can be modeled by adding a noise term, <i>ε<sub>i</sub>x</i>, to the right side of the equation: <i>y<sub>i</sub></i>=<i>Β<sub>i</sub>x</i>+<i>α</i>+<i>ε<sub>i</sub>x</i>. The most common regression model assumes that x is known exactly. In practice, regression works well if the relative magnitude of noise in <i>x</i> is much smaller than <i>y</i>. | ||
| + | |||
| + | |||
| + | The most common type of LR minimizes the value of the squared vertical distances between observed and predicted values | ||
| + | Model : | ||
| + | Assumptions: | ||
| + | the independent variable 𝑥 is known with certainty (or at least very much less error than 𝑦) | ||
| + | 𝜀 is an independent, random variable with 𝜇=0 | ||
| + | The distribution of 𝜀 is symmetric around the origin | ||
| + | the likelihood of large errors is less than small ones | ||
| + | Uncertainty in slope estimate | ||
| + | The error in slope 𝑊=𝛽 ̂−𝛽 | ||
| + | Variance of 𝑊 characterizes slope error | ||
| + | You can calculate a 95% (or other significance level) confidence interval for 𝛽 ̂ | ||
| + | What factors should the uncertainty depend on? | ||
| + | Estimate 𝜎^2 (𝑊): 𝑉^2 (𝑊)=(∑▒〖𝑟_𝑖^ 〗^2 )/((𝑁−2)∑▒〖(𝑥_𝑖−𝑥 ̅)〗^2 ) | ||
| + | N-2 is a “penalty” because regression line minimizes variance of residuals | ||
| + | If the interval contains 0, the null hypothesis that 𝛽=0 cannot be rejected | ||
| + | |||
| + | |||
| + | |||
| + | '''''Step 1: PLOT THE DATA''''' | ||
| + | |||
| + | ===Examine the residuals=== | ||
| + | |||
| + | * plot 'em for an informal look | ||
| + | * various tests of residuals exist | ||
| + | |||
| + | |||
| + | ==Overview of nonlinear regression== | ||
{| class="wikitable" style="text-align: center;" | {| class="wikitable" style="text-align: center;" | ||
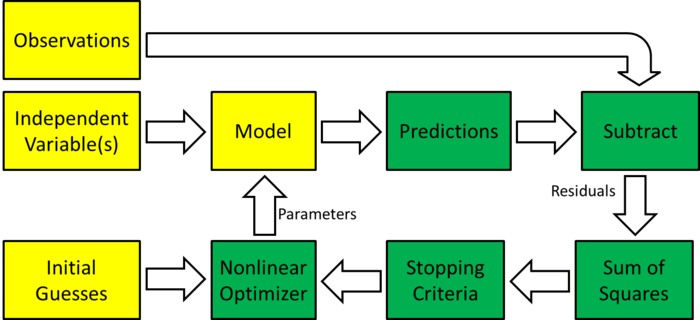
|[[Image:Regression block diagram.png|center|700px]] | |[[Image:Regression block diagram.png|center|700px]] | ||
| Line 6: | Line 49: | ||
|Block diagram of nonlinear regression | |Block diagram of nonlinear regression | ||
|} | |} | ||
| + | |||
| + | ==Practical nonlinear regression== | ||
{{Template:20.309 bottom}} | {{Template:20.309 bottom}} | ||
Revision as of 18:45, 5 January 2013
… the safe use of regression requires a good deal of thought and a good dose of skepticism
Review of linear regression
Linear Regression is a method for finding the magnitude of the relationship between two variables that co-vary. The technique assumes that a straight line characterizes the relationship between the two quantities: 𝑦=𝛽𝑥+𝛼, where 𝛽 is the true slope and 𝛼 is the true intercept. If two points on the line, (xi, yi); i = {1,2}, are precisely known, solving for the exact values of 𝛼 and 𝛽 is trivial. Unfortunately, all physical measurements include noise. The presence of noise precludes finding the exact values of 𝛼 and 𝛽.
The function of linear regression is to produce estimates of 𝛼 and 𝛽, denoted by α̂ and β̂, from a sample of N value pairs (xi, yi); i = {1, ..., N} that includes noise in the y-values. Thus, the samples can be modeled by adding a noise term, εix, to the right side of the equation: yi=Βix+α+εix. The most common regression model assumes that x is known exactly. In practice, regression works well if the relative magnitude of noise in x is much smaller than y.
The most common type of LR minimizes the value of the squared vertical distances between observed and predicted values
Model :
Assumptions:
the independent variable 𝑥 is known with certainty (or at least very much less error than 𝑦)
𝜀 is an independent, random variable with 𝜇=0
The distribution of 𝜀 is symmetric around the origin
the likelihood of large errors is less than small ones
Uncertainty in slope estimate
The error in slope 𝑊=𝛽 ̂−𝛽
Variance of 𝑊 characterizes slope error
You can calculate a 95% (or other significance level) confidence interval for 𝛽 ̂
What factors should the uncertainty depend on?
Estimate 𝜎^2 (𝑊): 𝑉^2 (𝑊)=(∑▒〖𝑟_𝑖^ 〗^2 )/((𝑁−2)∑▒〖(𝑥_𝑖−𝑥 ̅)〗^2 )
N-2 is a “penalty” because regression line minimizes variance of residuals
If the interval contains 0, the null hypothesis that 𝛽=0 cannot be rejected
Step 1: PLOT THE DATA
Examine the residuals
- plot 'em for an informal look
- various tests of residuals exist
Overview of nonlinear regression
| Block diagram of nonlinear regression |