Difference between revisions of "Nonlinear regression"
(→Review of linear regression) |
(→Review of linear regression) |
||
| Line 12: | Line 12: | ||
==Review of linear regression== | ==Review of linear regression== | ||
| − | Many useful models of physical systems are linear equations of the form <i>y</i> = <i>Βx</i> + α. Examples include Ohm's law for electrical resistors and Hooke's law for mechanical springs. Ohm's law models the relationship between the voltage (<i>V</i>) across and the current (<i>I</i>) through a resistor as a line: <i>V</i> = <i>IR</i>. The proportionality constant <i>R</i> is called the resistance. Hooke's law, <i>F</i> = <i>kx</i>, is a good model for the relationship between force (<i>F</i>) across and extension (<i>x</i>) of springs under many conditions. In order to apply these laws to real systems, the proportionality constant must be measured. | + | Many useful models of physical systems are linear equations of the form <i>y</i> = <i>Βx</i> + <i>α</i>. Examples include Ohm's law for electrical resistors and Hooke's law for mechanical springs. Ohm's law models the relationship between the voltage (<i>V</i>) across and the current (<i>I</i>) through a resistor as a line: <i>V</i> = <i>IR</i>. The proportionality constant <i>R</i> is called the resistance. Hooke's law, <i>F</i> = <i>kx</i>, is a good model for the relationship between force (<i>F</i>) across and extension (<i>x</i>) of springs under many conditions. In order to apply these laws to real systems, the proportionality constant must be measured. |
| − | + | Two points are needed to define a line. In the case of a spring, one point on the line is very easy to measure: (<i>F</i> = 0, <i>x</i> = 0). A second point could be obtained by applying a known force on the spring (by hanging a known mass on it in Earth's gravity, for example) and measure the its extension. Regardless of the two force conditions chosen, the procedure provides two, datapoints, (<i>x<sub>i</sub></i>, <i>y<sub>i</sub></i>); <i>i</i> = {1,2}. Solving for <i><i>Β</i> =<i>k</i> and <i>α</i> is trivial. | |
| − | + | Unfortunately, all physical measurements include noise. Measurement noise can be modeled by adding a random term, <i>ε<sub>i</sub></i>, to the right side of the model equation: <i>y<sub>i</sub></i> = <i>Β<sub>i</sub> x<sub>i</sub></i> + <i>α</i> + <i>ε<sub>i</sub>x</i>. The noise term introduces uncertainty into the measure values of <i>Β</i> and <i>α</i>. The presence of noise precludes finding the exact, true values of 𝛼 and 𝛽. | |
Linear Regression is a method for finding the magnitude of the relationship between two variables that co-vary. | Linear Regression is a method for finding the magnitude of the relationship between two variables that co-vary. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The technique assumes that a straight line characterizes the relationship between the two quantities: 𝑦=𝛽𝑥+𝛼, where 𝛽 is the true slope and 𝛼 is the true intercept. Some e | The technique assumes that a straight line characterizes the relationship between the two quantities: 𝑦=𝛽𝑥+𝛼, where 𝛽 is the true slope and 𝛼 is the true intercept. Some e | ||
| − | A simple way to find <i>α</i> and <i>β</i> is to measure the <i>y</i> at two different values of <i>x</i>, giving the | + | A simple way to find <i>α</i> and <i>β</i> is to measure the <i>y</i> at two different values of <i>x</i>, giving the |
| − | + | The function of linear regression is to produce estimates of 𝛼 and 𝛽, denoted by <i>α̂</i> and <i>β̂</i>, from a sample of N value pairs <span style="white-space: nowrap;">(<i>x<sub>i</sub></i>, <i>y<sub>i</sub></i>); <i>i</i> = {1, ..., N}</span> that includes noise in the <i>y</i>-values. The most common regression model assumes that x is known exactly. In practice, regression works well if the relative magnitude of noise in <i>x</i> is much smaller than <i>y</i>. | |
Revision as of 22:52, 5 January 2013
… the safe use of regression requires a good deal of thought and a good dose of skepticism
Review of linear regression
Many useful models of physical systems are linear equations of the form y = Βx + α. Examples include Ohm's law for electrical resistors and Hooke's law for mechanical springs. Ohm's law models the relationship between the voltage (V) across and the current (I) through a resistor as a line: V = IR. The proportionality constant R is called the resistance. Hooke's law, F = kx, is a good model for the relationship between force (F) across and extension (x) of springs under many conditions. In order to apply these laws to real systems, the proportionality constant must be measured.
Two points are needed to define a line. In the case of a spring, one point on the line is very easy to measure: (F = 0, x = 0). A second point could be obtained by applying a known force on the spring (by hanging a known mass on it in Earth's gravity, for example) and measure the its extension. Regardless of the two force conditions chosen, the procedure provides two, datapoints, (xi, yi); i = {1,2}. Solving for <i>Β =k and α is trivial.
Unfortunately, all physical measurements include noise. Measurement noise can be modeled by adding a random term, εi, to the right side of the model equation: yi = Βi xi + α + εix. The noise term introduces uncertainty into the measure values of Β and α. The presence of noise precludes finding the exact, true values of 𝛼 and 𝛽.
Linear Regression is a method for finding the magnitude of the relationship between two variables that co-vary.
The technique assumes that a straight line characterizes the relationship between the two quantities: 𝑦=𝛽𝑥+𝛼, where 𝛽 is the true slope and 𝛼 is the true intercept. Some e A simple way to find α and β is to measure the y at two different values of x, giving the
The function of linear regression is to produce estimates of 𝛼 and 𝛽, denoted by α̂ and β̂, from a sample of N value pairs (xi, yi); i = {1, ..., N} that includes noise in the y-values. The most common regression model assumes that x is known exactly. In practice, regression works well if the relative magnitude of noise in x is much smaller than y.
The most common type of LR minimizes the value of the squared vertical distances between observed and predicted values
Model :
Assumptions:
the independent variable 𝑥 is known with certainty (or at least very much less error than 𝑦)
𝜀 is an independent, random variable with 𝜇=0
The distribution of 𝜀 is symmetric around the origin
the likelihood of large errors is less than small ones
Uncertainty in slope estimate
The error in slope 𝑊=𝛽 ̂−𝛽
Variance of 𝑊 characterizes slope error
You can calculate a 95% (or other significance level) confidence interval for 𝛽 ̂
What factors should the uncertainty depend on?
Estimate 𝜎^2 (𝑊): 𝑉^2 (𝑊)=(∑▒〖𝑟_𝑖^ 〗^2 )/((𝑁−2)∑▒〖(𝑥_𝑖−𝑥 ̅)〗^2 )
N-2 is a “penalty” because regression line minimizes variance of residuals
If the interval contains 0, the null hypothesis that 𝛽=0 cannot be rejected
Step 1: PLOT THE DATA
Examine the residuals
- plot 'em for an informal look
- various tests of residuals exist
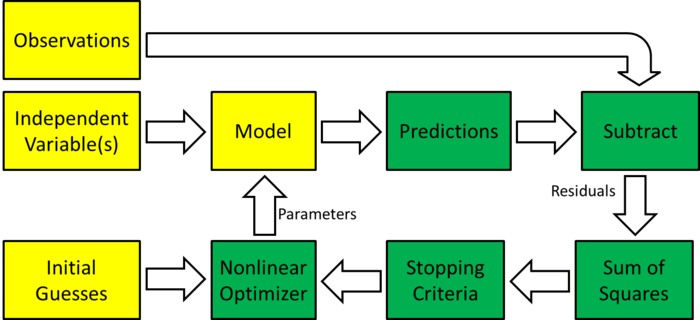
Overview of nonlinear regression
“If your program generates an error message rather than curve fitting results, you probably won’t be able to make sense of the exact wording of the message”
— Fitting Models to Biological Data using Linear and Nonlinar Regression by Motulsky and Shristopoulos
| Block diagram of nonlinear regression |